1、仪器简介
差热分析这项技术一直被广泛应用。既是一种例行的质量测试工具,也是一个研究工具。测量的是与材料内部热转变相关的温度、热流之间的关系。我公司的差热分析仪,具有重复性好、准确度高的特点,特别适合用于比热的精确测量。该设备易于校准,使用熔点低,快速可靠,应用范围非常广,特别是在材料的研发、性能检测与质量控制上。材料的特性,如玻璃化转变温度、冷结晶、相转变、熔融、结晶、产品稳定性、固化/交联、氧化诱导期等,都是差热分析仪的研究领域,根据实验参数以及实验需求来选择不同的型号。
差热分析仪应用范围有: 高分子材料的固化反应温度和热效应、物质相变温度及其热效应测定、高聚物材料的结晶、熔融温度及其热效应测定、高聚物材料的玻璃化转变温度,管材的抗氧化性能等。
2、仪器特点
1.全新的炉体结构,更好的解析度和分辨率以及基线稳定性;
2.仪器下位机数据实时传输,界面友好,操作简便;
3,仪器主要技术参数;
项目/型号 | DSC-2 | DSC-3 |
DTA量程 | 0~±2000μV |
温度范围 | 室温~1250℃ | 室温~1450℃ |
升温速率 | 0.1~100℃/min |
温度分辨率 | 0.01℃ |
温度波动 | ±0.01℃ |
温度重复性 | ±0.1℃ |
精确度 | 0.01μV |
灵敏度 | 0.01μV |
控温方式 | 升温、恒温(程序自动控制) |
曲线扫描 | 升温扫描,恒温扫描 |
气氛控制 | 2路气体自动切换 |
显示方式 | 24bit色7寸LCD触摸屏显示 |
数据接口 | 标准USB接口 |
仪器标准 | 配标准物质(锡),可自行矫准温度和热焓 |
备注 | 所有技术指标可根据用户需求调整 |





第4章 热分析动力学基础
4.1 引言
化学反应动力学大多被用来确定反应的速率方程(rate equation)和确定温度对反应速率的影响。
首先,可以通过动力学分析来确定反应的速率方程,用来描述反应过程中反应物或产物随着时间的转化程度,这类实验通常在恒定的温度下进行。通常将实验数据与根据理论动力学表达式计算出的预测值进行比较以确定最佳的速率方程, 该速率方程可以用来准确地描述实验测量过程。还可以通过这种动力学表达式推断出反应机制, 即反应物转化成产物的具体的化学反应步骤(包括可能的非常缓慢的速率控制步骤)。
另外,还可以用动力学分析来确定温度对反应速率的影响。在反应速率方程式中,温度变化对速率常数 k 的影响较大, 通常用阿伦尼乌斯(Arrhenius)方程来定量地捕述这种温度依赖性:
式中,k为速率常数;A为指前因子,单位为s-1;Ea为活化能,单位为J·mol-1;T为温度,单位通常为K;R为理想气体常数,数值为8.314。
长期以来,Arrhenius方程中的Ea和A的值已经得到了广泛的认可,其中活化能是对反应能量势垒的度量,而指前因子(也称频率因子,常用A表示)则是对导致产物生成频率的度量。在下面的内容中将进一步讨论Arrhenius参数的理论意义。此外,这些动力学参数提供了一种方便、可广泛使用的方法。这种动力学分析方法可以方便地比较不同体系的反应性,估算(并作适当的预测)在实验测量范围以外的温度下的反应性或稳定性。
4.2 理论基础
任何一种动力学研究的重要基础是以时间和温度为函数关系的一系列反应程度的测量数据。可以将在时间为t时的反应物和/或产物的总量(或与此相关的任何定量参数)看做对反应程度或反应分数用α表示)的度量;或者说,可与反应温度T一起测量α的变化率(dα/dt)。当根据这些可测量的参数来定义α时,需要知道反应的化学计量关系, 还需要考虑任何并列的或连续的速率过程的贡献。
等温条件广泛地应用于动力学研究,通过在几个不同的恒定温度下测量待测的反应速率可获得Arrhenius参数。在热分析领域,由程序升温实验、动态或非等温实验中获得动力学信息的方法已受到越来越广泛的关注。这些实验通常在一系列不同的、恒定的加热速率(β=dT/dt)下进行,主要测量一些直接与反应分数α相关的物理量(例如质量、热效应等)。
4.2.1 均相反应的动力学
对于等温均相反应的动力学研究而言,其通常是在恒定温度下测量一种(或多种)反应物或产物的浓度随时间的变化关系。速率方程的一般形式如下:
式中,f(C)和f(α)分别为浓度和转化率的表达式。
等式(4.2)为以生成物的浓度表示的速率方程式,而等式(4.3)则是以生成物的反应进度(转化率)表示的速率方程式。
4.2.2 非均相反应动力学
非均相反应与均相反应有着很大的差别。对于涉及固体的反应而言,化学反应一般优先发生在晶体表面或反应物和产物之间的过渡相区域(即反应界面),在该区域一般反应能力局部增强。反应物组分一般位于固体产物的表面附近,以增加产物相的数量。
反应界面是在成核过程中产生的,随后通过核生长进入其所在的由晶体组成的反应物原料中。由于界面的反应性保持不变,因此在其整个反应过程中,界面线性推移或生长的速率保持恒定。因此,在这种类型的反应中的反应固体内的产物形成速率与反应物-产物界面的总面积成正比。
与均相反应不同,在涉及固体反应速率过程的动力学分析中,浓度项通常不再具有明确的物理意义。在反应物晶体的内部空间内,各处的浓度均相同、而一旦超出这些边界,则发生化学变化的物质的数量均为零。由于存在浓度的空间变化, 因此材料在扩散控制反应中的分布是不均匀的。因此,固体组分的反应性随着位置和时间的变化而不同, 这意味着当该组分位于活性界面的影响区域内时,反应发生的概率将会显著增加。因此,在进行动力学分析时需要考虑系统变化的活性界面影响,以及由反应物或产物物质的扩散速率所带来的影响或控制。
在定量描述反应进行程度的表达式中,为了描述上的方便仍习惯采用如等式(4.3)所示的表达式,等式中的f(α)习惯称为机理函数或者模式函数。
在与固态反应的动力学有关的文献中,“机制”或“机理”这个术语被使用得相当模糊不清。一些研究者使用这个术语来描述速率方程与其数据的拟合程度,而另一些研究者则用这个术语来描述反应物和生成物在反应过程中的结构变化过程。对于前一种情形而言,“动力学模型”是更准确的描述形式。许多研究者倾向于采用均相动力学的方式来描述反应物转化成产物的反应的反应级数用来强调固态反应的化学基础,但在实际应用时往往忽略固态反应的化学基础,倾向有利于确定动力学模型的数学分析。
4.3 热分析动力学方程式
对于一个等温下的固态反应而言,通常可用下式描述其反应速率:
式中,A为指前因子(也称频率因子);Ea为活化能;T是绝对温度,单位为K;R是理想气体常数;f(α)是机理函数;α是转化率。
对于由热重法得到的数据而言,α定义为下式的形式:
式中,m0是反应开始时的初始质量,mt是时间t时的质量,m∞是反应结束时的最终质量。
可以通过上述速率方程式(式(4.1))由等温动力学数据获得反应过程中的动力学参数(机理函数、A和Ea)。对于由非等温实验得到的实验数据而言,可以通过利用下式将式(4.1)进行变形,从而得到在恒定的加热速率下的反应速率作为温度的函数的非等温下的速率表达式:
式中,dα/dT为非等温反应速率,dα/dt则为等温反应速率,dT/dt是恒定加热速率,通常用β表示。
将式(4.1)代入式(4.6),可以得到恒定加热速率下的非等温速率方程式的微分形式:
分离变量,并积分等式(4.4)和等式(4.7)可以分别得到等温和非等温条件下的速率方程的积分形式,如下式所示:
式中,g (α)是积分形式的机理函数,定义为
文献中表示这些机理函数的符号经常出现不一致的现象,在一些出版物中经常出现f(α)和g (α)的定义颠倒的现象。
4.4常见的机理函数及其物理意义
根据其机理不同,在目前固态反应动力学研究中广泛使用的机理函数中,通常分为成核、几何收缩、扩散和级数反应四种类型。表4.1中分别列出了常见的机理函数的微分表达式f(α)和积分表达式g (α)。
表4.1 常用的动力学机理函数
函数号 | 函数名称 | 机理 | 积分形式 | 微分形式 |
1 | 抛物线法则 | 一维扩散,减速α-t曲线 |
|
|
2 | Valensi | 二维扩散,圆柱形对称,减速α-t 曲线 |
|
|
3 | Jander方程 | 二维扩散,n=1/2 |
|
|
4 | Jander方程 | 二维扩散,n=2 |
|
|
5 | Jander方程 | 三维扩散,n=1/2 |
|
|
6 | Jander方程 | 三维扩散,球形对称,减速α-t 曲线, n=2 |
|
|
7 | G-B方程 | 三维扩散,球形对称,D4,减速α-t 曲线 |
|
|
8 | 反Jander方程 | 三维扩散 |
|
|
9 | Z-L-T方程 | 三维扩散 |
|
|
10 | Avrami-Erofeev方程 | 随机成核和随后生长,A4,S形αt曲线,n =1/4,m=4 |
|
|
11 | Avrami-Erofeev方程 | 随机成核和随后生长,A3,S形α-t曲线,n =1/3,m=3 |
|
|
12 | Avrami-Erofeev方程 | 随机成核和随后生长,n=2/5 |
|
|
13 | Avrami-Erofeev方程 | 随机成核和随后生长,A2,方程S 形α-t曲线,n=1/2,m=3 |
|
|
14 | Avrami-Erofeev方程 | 随机成核和随后生长,n=2/3 |
|
|
15 | Avrami-Erofeev方程 | 随机成核和随后生长,n=3/4 |
|
|
16 | Mample 单行法则,一级 | 随机成核和随后生长,假设每个颗粒上只有一个核心A1,F1,S形α-t曲线,n =1,m=1 |
|
|
17 | Avrami-Erofeev方程 | 随机成核和随后生长,n=3/2 |
|
|
18 | Avrami-Erofeev方程 | 随机成核和随后生长,n=2 |
|
|
19 | Avrami-Erofeev方程 | 随机成核和随后生长,n=3 |
|
|
20 | Avrami-Erofeev方程 | 随机成核和随后生长,n=4 |
|
|
21 | P.T方程 | 自催化反应,枝状成核,An,B1,S形α-t曲线 |
|
|
22 | Mampel Power法则 (幂函数法则) |
|
|
|
23 | Mampel Power法则 (幂函数法则) |
|
|
|
24 | Mampel Power法则 (幂函数法则) |
|
|
|
25 | Mampel Power法则 (幂函数法则) | 相应边界反应(一维),R1,n=1 |
| 1 |
26 | Mampel Power法则 (幂函数法则) |
|
|
|
27 | Mampel Power法则 (幂函数法则) |
|
|
|
28 | 反应级数 |
|
|
|
29 |
| 相边界反应,球形对称,R3,减速α-t曲线,n=1/3 |
|
|
30 | 收缩球状(体积) | 相界面反应,圆柱形对称,R2,减速α-t曲线,n=2(二维) |
|
|
31 |
| 相边界反应,圆柱形对称,R2,减速α-t曲线,n=1/2 |
|
|
32 | 收缩圆柱体(面积) | 相界面反应,圆柱形对称,R2,减速α-t曲线,n=2(二维) |
|
|
33 | 反应级数 |
|
|
|
34 | 反应级数 |
|
|
|
35 | 反应级数 |
|
|
|
36 | 反应级数 | 化学反应,F2,减速α-t曲线
|
|
|
37 | 反应级数 | 化学反应 |
|
|
38 | 反应级数 | 化学级数为2/3级 |
|
|
39 | 指数法则 | E1,n=1,加速α-t曲线 |
|
|
40 | 指数法则 |
|
|
|
41 | 反应级数 | 化学反应,F3,减速α-t曲线,n=3 |
|
|
42 | S-B方程 | 固相分解反应SB(m,n) |
|
|
43 | 反应级数 | 化学反应, |
|
|
44 | J-M-A方程 | 随机成核和随后生长,An,JMA(n) |
|
|
45 | 幂函数法则 | P1,加速α-t曲线 |
|
|
注:①Ginstling=Brounstein方程;②Zhuralev-Lesokin-Tempelman方程;③Prout-Tompkins方程;④函数1和27称谓不同,形式不同;⑤Šest佗k-Berggren方程;⑥Johnson-Mehl-Avrami方程。
4.4.1 常见的机理函数
通常使用热重法研究固态反应动力学,也可以通过其他分析方法,如差示扫描量热法(DSC)、变温粉末X射线衍射法(XRD)和变温核磁共振法(NMR)。无论使用何种分析方法,在进行动力学分析时,测量的参数必须能够转化为可以在动力学方程中使用的转化率α。
另外, 可以通过模型拟合或无模型(等转化率法)方法进行等温或非等温过程的动力学分析。由于通过等转化率法或无模型方法能够计算得到没有模型假设的Ea值,近年来使用这些方法进行动力学分析的研究呈现增加的趋势。然而随着研究的深入,一些研究工作者注意到这两种方法仍存在一些不足之处,即对一个固态反应进行完整的动力学分析通常需要反应机理函数来进行全面的动力学描述。在文献[8]中综合比较了不同的固态动力学分析方法。
4.4.2 机理函数的机理
机理函数是对实验的动力学过程的理论数学描述。在固态反应中,可以用机理函数来描述特定的反应类型,并在数学上将其转化为速率方程。目前在固态动力学的研究中已经提出了许多机理函数,这些机理函数大多是基于某些特定的机理假设而发展起来的。除此之外,还有一些其他机理函数基于经验假设,它们的提出主要出于方便数学分析的角度考虑,而从机理的角度则往往很难解释这些机理函数。通过动力学分析,可以由这些不同的机理函数得到不同的速率表达式。
在均相反应动力学(例如气相或液相)中,通常通过动力学研究直接获得可用于描述反应进程的速率常数。除此之外,通过反应动力学机理的研究以及速率常数随温度、压力或反应物/产物浓度的变化的研究通常有助于揭示反应发生的机理, 而这些机理通常涉及不同程度的反应物转化成产物的多个具体的化学步骤。然而,在固态动力学中,由于与每一个反应步骤相关的信息通常难以获得,因此机理解释通常需要确定合理的反应模型。事实上,反应的机理函数的选择应该得到其他互为补充的技术,例如显微镜、光谱、X射线衍射等实验数据的支持才能证明其更为合理。
4.4.3 机理函数的分类
对于等温实验而言,通常根据其等温曲线的图形形状(α-t 或dα/dt-α曲线)或其机理假设对动力学分析时用到的机理函数进行分类。基于这些曲线的形状,动力学机理函数可以分为加速、减速、线性或S形机理函数(图4.1)。加速模型机理函数是其中反应速率(dα/dt)随着反应进行而增加的一类机理函数,而减速模型机理函数的反应速率则随着反应进程的增大而减小(图4.1(b)~(d))。对于线性模型机理函数,反应速率速率对于反应进程α保持恒定(图4.1(e))。S形模型机理函数的反应速率和α之间呈现钟形关系(图4.1(f))。
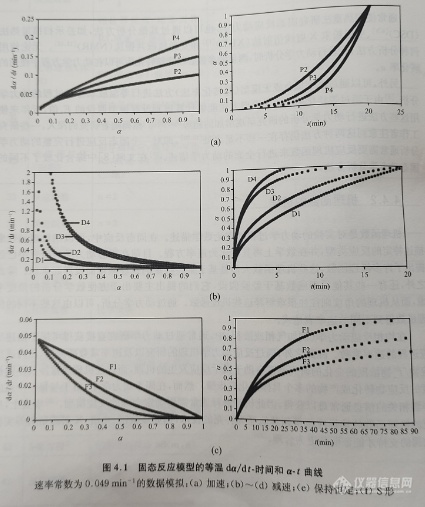

对于非等温实验而言,反应进度与温度曲线(即α-T曲线)的形状不如其等温的α-t曲线明显。图4.2示出了由等式(4.7)和等式(4.9)计算得到的非等温α-T曲线和dα/dT-α曲线。在一些特殊的情况下,对于由等温实验得到的数据而言,图4.1中的模型所对应的机理函数可以使用α或dα/dt对约化时间曲线作图;而对于非等温实验下得到的实验数据而言,图4.2中的模型所对应的机理函数则可以使用主曲线方法进行作图。这些用于图形表示的方法是一种简化的数据处理方法,通常用于由特定数据集直观地确定最佳的机理函数。

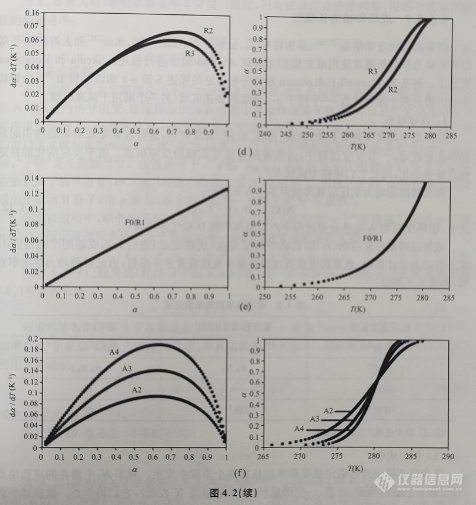
基于机理假设,通常将机理函数分为成核、几何收缩、扩散及级数反应几类,如表4.1所示。
4.4.4 机理函数的推导
如前所述,机理函数的推导基于常见的几种反应机理,主要包括成核、几何形状、扩散和级数反应。Sestak 和 Berggren 提出了一种数学形式,表示单个一般表达式中的所有模型:
式中,m、n和p均为常数。通过改变这三个变量的值,等式(4.11)可以用来表示任何一种机理函数。
在下面的内容中讨论常用的几类机理函数的推导和理论意义。
4.4.4.1 成核和核生长模型
许多固态反应如结晶、晶型转变、分解、吸附、水合和去溶剂化等过程的动力学分析通常使用成核模型尤其是Avrami模型进行描述。Skrdla和 Robertson提出了一种基于Maxwell-Boltzmann能量分布理论的描述S形α-t曲线的模型,由该模型可以得到两个速率常数:一个用于α-t曲线的加速区域,另一个则用于减速区域。
1.成核过程
晶体由于其自身具有杂质,表面、边缘、位错、裂纹和点,这些现象导致的缺陷将引起其局部能量波动。在反应过程中,这些缺陷是反应成核的反应位点。由于反应活化能在这些点处最小化,因此它们被称为成核点。
常见的固态动力学反应通常按照如下方式进行:
式中,固体反应物A在热分解过程中产生固体产物B和气体产物C。
成核过程是在反应物(A)的晶格中的反应点(成核位点)进行而形成新的产物相(B)。在进行动力学计算时,通常假设成核过程是单步成核或者多步成核, 由此得到动力学速率方程,如表4.2所示。
表4.2 成核速率的数学表达式
成核速度定律 | 微分形式dN/dT | 积分形式 N |
指数 |
|
|
线性 |
|
|
瞬时 | ∞ |
|
幂级 |
|
|
注:1单步成核;2多步成核。
(1)单步成核
单步成核模型通常假定成核和核生长在单个步骤中发生。对于N0个潜在的成核位点(具有相等的成核概率)而言,一旦形成核(核的数量用N表示),它们将生长。成核速率属于一级反应,可以用下式表示:
式中,N为在时间t时存在的成核的数量;kN为成核的速率常数。
对等式(4.13)分离变量并积分,可得下式:
等式(4.13)微分后可得成核的指数速率:
当kN无限小时,式(4.15)中的指数项趋近于1,并且成核速率近似常数,由此可得到成核的线性速率如下式所示:
当kN非常大时,表明成核速率非常快。此时,所有成核位点迅速成核,可用下式表示成核的瞬时速率:
(2)多步成核
多步成核通常假定需要几个不同的步骤来完成核的生长过程。因此,产物B的形成将在A的晶格内诱导应变,这使得形成的B核的小聚集体变得不稳定,并且易产生逆反应使B再形成反应物A。如果形成的B核的数量高于临界数量(mc),则可以克服应变。因此,我们可以定义两种类型的核:“子核”和“生成核”。当B核的颗粒数量低于临界数量(m<mc)时,“子核”是亚微观尺寸。在该条件下,“子核”将发生逆反应形成反应物A或当B核的颗粒数量高于临界数量(m>mc)时进一步长大成为“生成核”。因此,“子核”必须积累相当数量的生成物B分子(用p表示)后才有可能进一步转变成为“生成核”。
在成核过程中,单个分子依次累积,直至p个分子时形成一个“生成核”(此时分子数n
在p个分子已经完成(此时分子数n>p)后,进一步累积分子引起核生长的速率常数(kg)可以表示为
假设核生长的速率大于核形成的速率(即kg>ki),根据Bagdassarian的研究结果,如果形成“生成核”需要β次连续反应,并且每次的概率为ki,则在时间t形成的核的数目可用下式表示:
式中, 。
。
等式(4.20)微分后,可得到下式:
式(4.21)即为表4.2中表示成核的幂律方程。Allnatt 和Jacobs也曾推导出了方程(4.21),但是他们假定在达到临界尺寸n=p之前,分子连续累积形成“生成核”过程中的速率常数不相等。
2.核生长过程
可以用由核生长形成的核半径表示核生长速率(用G(x)表示)。G(x)通常随着核的尺寸大小而变化。例如,通常为亚显微尺寸的小核的生长速率与大核的生长速率不相同。尺寸非常小的“子核”由于其不稳定性较差,生长速率较低,容易发生逆反应变回到反应物状态。
在时间t[r(t,t0)]时的稳定的核(即“生成核”)的半径可以用下式来表示:
式中,G(x)是核生长速率,t0是“生成核”的形成时间。
除了核半径之外,还应考虑在核生长过程中的两个重要方面:核形状(σ)和核的生长维数(λ)。在考虑这些因素后,我们可以用单个核占据的体积(v(t))来定量表示核生长速率。
因此,在时间t0形成的稳定核在时间t占据的体积v(t)可根据下式得到:
式中,λ为生长尺寸的数量(即λ=1,2或3),σ为形状因子(当假设为圆球时,σ=4π/3),r为在时间t时核的半径。等式(4.23)给出了由单个核所占据的空间体积;所有核占据的总体积(V(t))可以通过由成核速率(dN/dt)、生长速率(V(t,t0))以及核生长的不同的初始时间组成的方程进行计算得到,可以用下式来表示:
式中,V(t)是所有生长核的体积,dN/dt是成核速率。将式(4.22)代入(4.23),并将式(4.23)代入式(4.24)可以得到下式:
上述等式(4.25)针对成核和/或核生长速率定律的任何组合进行积分,可以得到如表4.1所列的速率表达式形式(g(α)=kt)。然而,由于成核和核生长之间不存在函数关系,按照这种方法并非总能奏效。因此,关于成核(dN/dt)和核生长(V(t))速率方程通常需要按照以下的方法进行假设。
3.幂律模型(P)
对于成核速率遵循幂定律(等式(4.21))并假设核生长为常数(即G(x)=kG)的简单情况,等式(4.25)可以变形为下式;
对等式(4.26)进行积分展开,可得到下式:
分别定义
和
则等式(4.27)可简化表示为下式:
由于V(t)与反应进程α成正比,因此a可表示为
在等式(4.31)中,C为等于1/V0(V0为初始体积)的常数。
由等式(4.21)和等式(4.22),可以得到下式:
等式(4.32)可以变形为
定义
则等式(4.33)可以简化为下式:
重新排列式(4.35)可得下式:
等式(4.36)可以用来表示各种幂律模型机理函数(P模型)(见表4.1)。由于这些机理函数假设恒定的核生长而不考虑核的生长限制,因此它们通常被应用于曲线的加速周期的分析。
4.Avrami-Erofeyev模型(A模型)
在任何一个固态分解过程中,核的生长都会受到一定的限制。目前已经明确存在两种类型的限制作用,如图4.3所示。这两种作用分别为:

(1)摄入作用:这种作用通过现有的核的生长来消除潜在的成核位点;摄入位点由于其包含在生长核中而从不产生生长核。摄入的核通常被称为“幽灵”核。
(2)聚集作用:当两个或更多个生长核的反应区合并时,反应物/产物界面消失引起的相互作用。
可以用以下表达式确定成核位点的数量:
式中,N0为可能的成核位点的总个数,N1(t)是在时间t时的核的实际数目,N2(t)是摄取的核的数目,N(t)是形成的核的个数。
由等式(4.37)可以得到指数修正的成核速率(dN/dt)方程。然而,如果将该成核速率代入等式(4.24),则所得到的表达式没有解析解,这个问题可以通过忽略摄取作用和核聚结作用的扩展转换分数(α′)来解决。α′也就是我们之前在等式(4.35)中 定义的转换分数。因此,α′≥α。我们可以通过与α′值的关系来评价α的值。
定义的转换分数。因此,α′≥α。我们可以通过与α′值的关系来评价α的值。
扩展的转化率(α')与实际的转化率(α)之间存在着以下的关系:
等式(4.38)积分后,可得下式;
将等式(4.25)中的α'的值代入式(4.39)中,可得下式:
重新排列式(4.40),可得下式:
Erofeyev(也作Erofe′ev或Erofeev)还按照不同的方法导出对于n=3时的等式(4.41)的特殊情况。因此,等式(4.41)可归功于Avrami和Erofeev,这二位研究者提出了不同的n值对应的不同的Avrami-Erofeev(A)机理函数(见表4.1)。在文献中,通常称这些A类机理函数为JMAEK机理函数,JMAEK分别代表Johnson、Mehl、Avrami、Erofeev和Kholmogorov五位研究者,以纪念他们对A类机理函数的发展所做出的杰出贡献。
5.自催化模型(B1模型)机理函数
在均相动力学中,当产物对反应有催化作用时发生自催化。这种现象通常在当反应物在产生所谓的“支化”的反应期间再生时发生。随着反应的进行,反应物最终被消耗,反应进入其将停止的“终止”阶段。
在固态动力学中,也可以看到类似的现象。如果核生长由于在反应界面(即分支)处形成缺陷如位错或裂纹而促进连续反应, 则自催化发生将发生在固态动力学中。当反应开始扩展到已经分解的材料中时,自催化过程将终止。Prout和Tompkins基于高锰酸钾热分解期间产生了相当大的晶体裂纹的现象提出了自催化模型(B1)。
在自催化反应中,成核速率可以用下式表示:
等式(4.42)中,kB是支化反应的速率常数,kT是终止反应的速率常数。如果忽略kNN0,则等式(4.42)可以变形为下式:
这种特例主要可能发生在以下两种情况之一:
(1)kN非常大,使得初始成核位点迅速耗尽,并且dN/dt的计算在N0位点耗尽之后的时间间隔足够短;
(2)kN非常小,使得kNN0可以忽略不计。
概括来说,反应速率与核的数目相关,可用下式表示:
式中,k′为反应速率常数。
Prout和Tompkins发现,对于高锰酸钾分解而言,α-t曲线的形状是S形的。因此,存在一个拐点(αi,ti)可以改变dN/dt的数值符号。由在该拐点(即kB=kT)处需满足的边界条件,定义kT如下:
将等式(4.45)代入等式(4.43),可以得到下式:
由于dN/dα=dN/dt·dt/dα,因此将等式(4.44)、等式(4.46)分别代入该式中,则可以得到下式:
等式(4.47)中定义了k′′=kB/k′。
假设kB独立于α,等式(4.47)分离变量并积分,可得下式:
将式(4.48)代入式(4.44)可得到下式:
Prout和Tompkins假设αi=0.5,则等式(4.49)可以简化为下式:
对等式(4.50)分离变量并积分,可得到下式:
式中,c为积分常数。
等式(4.51)即为我们通常所说的Prout-Tompkins 模型(也称B1模型)(见表4.1),使用该类型的机理函数可以很好地拟合固体高锰酸钾的热分解过程。
注意:与其他类型的机理函数不同,在下限α=0时,等式(4.50)的积分不受限制,该值为负无穷大,由此导致积分常数出现在Prout-Tompkins方程式(等式(4.51))中。因此,在一些文献中关于这个方程的表示没有常数项,如下式所示:
由于由等式(4.52)可以得到当α<0.5时的负的时间值(图4.4),因此这样将会导致混乱。为了克服这个问题,需要在式(4.41)中带有积分常数c,这样得到的曲线将向正的时间值移动。目前对于什么是积分常数没有明确的要求。Prout和Tompkins使用最大速率(即曲线拐点)所需的时间tmax表示c,而与Carstensen使用的t1/2表示相比,这两种方法得到的结果差别不大。如果使用α=0.01所对应的时间30.21 min进行计算得到图4.4的模拟结果,使用其他值得到的结果也同样有效。
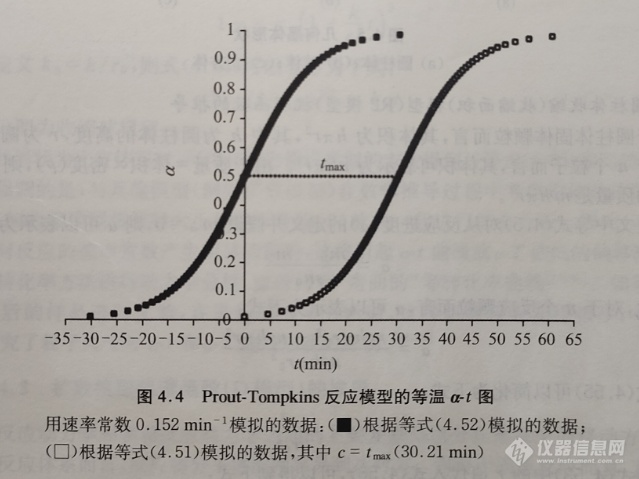
Prout-Tompkins模型由于在推导过程中需要的假设而受到一些争议,一些研究者针对这个问题提出了一些其他形式的建议。Skrdla认为成核和支化反应是两个独立的过程(也可认为虽独立但可以相互耦合),具有两个不同的速率常数,并基于此提出了自催化速率表达式。如果成核和支化速率常数相等,则由他们所提出的表达式可以得到Prout-Tompkins模型。Guinesi等人的研究结果表明,钛(IV)-EDTA在加热过程中的脱羧分为两个步骤,第一个步骤为B1模型,而第二个步骤则为R3模型。
4.4.4.2 几何收缩模型(R模型)机理函数
几何收缩模型假设成核在晶体的表面上快速发生,通过所得到的反应界面向晶体中心的推进来控制分解速率。根据晶体形状,可以导出不同的数学模型。
对于任何晶体颗粒,存在以下关系:
式中,r为在时间t时的半径,r0为在时间t0时的半径,k为反应速率常数。
如果假定固体颗粒具有圆柱形或球形/立方体形状(见图4.5),则可以分别推导得到圆柱体收缩的面积或球体/立方体的收缩体积模型机理函数。研究表明,一水草酸钙的脱水过程遵循几何收缩模型。
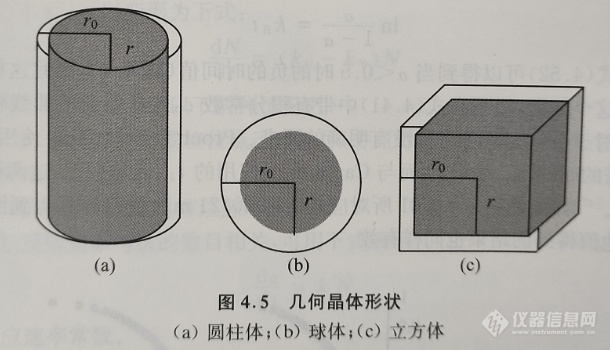
1.圆柱体收缩(收缩面积)模型(R2模型)机理函数的推导
对于圆柱体固体颗粒而言,其体积为hπr2,其中h为圆柱体的高度,r为圆柱体的半径。对于n个粒子而言,其体积可表示为nhπr2。由于质量=体积×密度(ρ),则n个圆柱状颗粒的质量是nρhπr2。
由上文中等式(4.5)对从反应进度(α)的定义并假设m∞=0,则α可以表示为下式:
因此,对于n个反应颗粒而言,α可以表示为下式:
等式(4.55)可以简化为下式:
将等式(4.53)中的r值代入式(4.56),可以得到下式:
将等式(4.57)重新排列,可以得到下式:
定义k0=k/r0,则等式(4.58)可以变形为下式:
等式(4.59)即为收缩圆柱模型。
2. 收缩球/立方体(收缩体积)模型(R3模型)的推导
当假设固体颗粒为球形或立方体形状时,可以推导出收缩球/立方体模型的机理函数。当颗粒为球形时,已知球体的体积为4πr3/3,对于n个粒子,其体积为4nπr3/3。由于每个球体的质量=体积×密度(ρ),则n个球形颗粒的质量可以用下式表示:
对于涉及n个粒子的反应,将等式(4.60)代入等式(4.54)中,则可以得到下式:
等式(4.61)可化简为
将等式(4.53)中的r值代入等式(4.62)中,则可以得到下式:
对等式(4.63)进行重新排列,可以得到下式:
仍然定义k0=k/r0,则式(4.64)可以变形为下式:
等式(4.65)即为收缩球模型。
当颗粒形状为立方体形时,可用与球形假设类似的方法得到与等式(4.65)相同的表达式。需要强调的是,与其他模型(例如扩散模型)在数学推导过程中考虑固体品体的几何形状相比,几何收缩模型将粒径大小与速率常数(k)放在一起进行综合分析。因此,不同粒径的样品将对反应的速率常数产生明显的影响,这将引起α-t曲线或α-T曲线的偏移现象。如果使用等转化率方法进行动力学分析,也将得到“弯曲的”等转化率曲线。如果使用分样筛筛分后的样品进行实验,在进行动力学分析时,这种影响将会变得很小。Koga 和Criado研究了粒子尺寸对α-t和α-T曲线形状的影响。
4.4.4.3 扩散模型机理函数(D模型)的推导
均相反应动力学和多相反应动力学之间的主要差别是组分在体系中的移动方式不同。对于均相反应体系而言,反应物分子彼此间容易到达对方。而对于固态反应而言, 其通常发生在晶格之间或者分子必须渗透到晶格中,分子的运动受到限制并且还与晶格缺陷密切相关。当反应速率受反应物到反应界面的扩散或来自反应界面的产物的移动控制时,产物的界面层增加。除了少数可逆反应或当发生大的放热或消耗时,固态反应通常不通过质量传递控制。当反应物在单独的晶格中时,扩散通常在两个固体相互反应时的反应速率中发挥作用。Wyandt和Flanagan的研究表明磺酰胺-氨复合物的去溶剂化过程遵循扩散模型。他们的研究结果还发现,由计算得到的氨复合物的去溶剂化活化能与磺酰胺的固有酸度之间存在一定的相关性,这种现象是由于磺酰胺(酸)和氨(碱)在固态下的酸-碱相互作用引起的。药物的pKa与氮-药物相互作用的强度成反比,其反过来影响去溶剂化活化能。
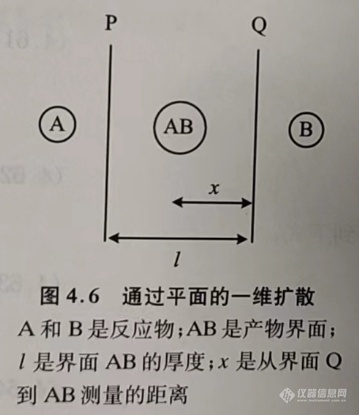
在扩散控制反应中,产物形成速率与产物层的厚度成比例减小。对于金属氧化反应而言,与界面移动有直接关系,该过程如图4.6所示。根据图4.6,一定质量的反应物B在时间dt时移动穿过界面P(单位面积),生成产物AB,可以用下式表示速率方程式:
式中,MAB和MB分别是AB和B的分子量,D是扩散系数,F是产物AB的密度,l是产物层AB的厚度,C是B在AB中的浓度,x是从接口Q到AB的距离。
假设AB中B的线性浓度呈梯度,即
式中,C2和C1分别是界面P和Q处的B的浓度,则方程(4.66)可以变形为
分离变量并积分等式(4.68),可以得到下式:
假设
则等式(4.69)变为
等式(4.71)被称为抛物线定律。最简单的速率方程是针对不涉及形状因子(例如,一维)的无穷平面,其中转化进度α与产物层厚度l成正比。因此, 等式(4.71)可以变形为
式中,k′是常数。等式(4.72)表示一维扩散(D1)模型。
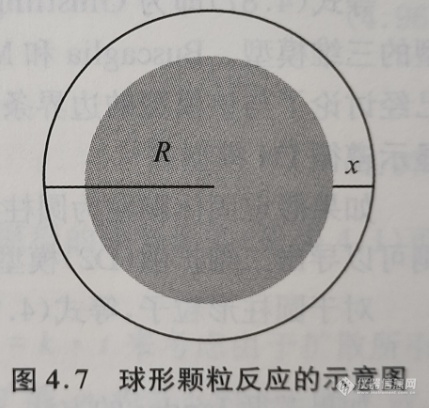
三维扩散(D3)模型是基于球形固体颗粒的假设(图4.7)。使用等式(4.54)和等式(4.60)的包括n个球形颗粒的反应的转化率为
式中,x是反应区的厚度。简化后,等式(4.73)可以变形为
等式(4.74)可以重新排列为
Jander 使用抛物线定律(等式(4.71))来定义x。因此,将等式(4.75)(将x平方后)代入等式(4.71),可以得到以下等式:
假设
则等式(4.76)可以变形为以下的D3(Jandcr)模型:
Ginstling-Brounshtein的研究工作表明,使用抛物线定律(针对平面表面导出)的Jander 模型(方程(4.78))被过度简化并且仅在低转换值(即低x/R值)时成立。Fick 第一定律在球体中的径向扩散的稳态解是
式中,C(r)是r的特定值处的反应物浓度(a1是表面r=a处的扩散物质的浓度,C2是表面r=b处的扩散物质的浓度。假定界面处的反应以比扩散快得多的速率发生,此时C1≈0。因此,等式(4.79)可以变形为
取上述方程相对于r的导数,当r= a时,有
根据图4.7,a=R-x,b=R,则等式(4.81)可变形为
反应区推进速率dx/dt可以与dC/dr相关:
式中,D是扩散系数,ε是等于ρn/μ的比例常数(ρ和μ分别是产物的比重和分子量,n是反应的化学计量系数)。将等式(4.82)代入等式(8.83)得到
其可以被重写为
式中,k=DC2/ε。
分离变量并积分等式(4.85),可得
用等式(4.75)中的x的值代替等式(4.86)中的x,并重新给出
等式(4,87)即为Ginstling-Brounshtein(D4)模型的数学表达式。D4模型是另一种类型的三维模型。Buscaglia和Milancse提出了Ginstling-Brounshtein模型的一般形式,并且已经讨论了与该模型的边界条件相关的限制。 四氧化三锰(Mn3O4)和碳酸钠之间的反应显示遵循D4模型。
如果假定固体颗粒为圆柱形,并且扩散通过具有增加的反应区的圆柱形壳体径向发生,则可以导出二维扩散(D2)模型。D2模型可以使用用于D3模型的相同的一般方法导出。
对于圆柱形粒子,等式(4.75)可以定义为
如果遵循Jander的方法,得到的方程是
式中,k′=k/R′′。等式(4.89)不是文献中通常使用的D2模型。通常使用的D2模型是根据 Ginstling-Brounshtein 方法导出的,Fick第一定律在圆柱体中的径向扩散的稳态解是
式中,C(r)是在r的特定值处的反应物浓度(a 1是在表面r= a处的扩散物质的浓度,C2是表面r=b处的扩散物质的浓度,假设界面处的反应以比扩散快得多的速率发生,使得C≈0。因此,等式(4.90)变形为
对等式(4.91)相对于r求导,当r= a时,有如下形式的关系式:
根据图4.8,a =R-x和b=R,因此等式(4.92)变为

将等式(4.93)代人等式(4.83),可以得到下式:
式中,k=DC2/ε。用等式(4.75)中的x代替等式(4.94)中的x的值,并重新排列,可得
等式(4.75)的导数为
将方程(4.96)代入方程(4.95)中,并重新排列,可得
式中,k′=4k/R2。等式(4.97)为D2模型的微分形式。D2模型的积分形式(见表4.1)可以通过分离变量和积分等式(4.97)得到。
最后,可以通过修正后的JMAEK模型[-ln(1-α)]1/n=k·t来考虑由于扩散所引起的影响。其中,n为1.5时为一维扩散,n为2时为二维扩散,n为2.5时为三维扩散。扩散系数(D)包括在反应速率常数(k)中。
4.4.4.4 基于反应级数的模型(F)
基于反应级数的模型是最简单的模型,因为它们类似于均相反应动力学中使用的模型。在这些模型中,反应速率与反应物的浓度、反应物残余量或残留分数的幂指数n(即反应级数)成正比。需要特别指出,一些热分析动力学分析方法将机理函数强制假设为基于反应级数的模型,由此可能会带来错误的分析结果。
通常用以下方程式表述基于反应级数的模型:
式中,dα/dt是反应速率,k是速率常数,n是反应级数,
如果在等式(4.98)中n=0,则获得零级反应模型(即F0或R1)模型,此时等式(4.98)变形为下式:
在分离变量和积分之后,等式(4.99)可变形为
当n=1时,由等式(4.98)可以得到一阶反应模型(F1模型)的表达式,此时等式(4.98)可以变形为
对等式(4.101)进行分离变量和积分,可以得到以下一阶积分表达式:
该一阶模型也称为Mampel模型,为Avrami-Erofeev(A)模型的特殊情况(当n=1时)。可以通过相似方法得到二阶(当n=2时)和三阶(当n=3时)的机理函数(表达式如表4.1所示)。Lopes等人的研究结果表明,钆(Ⅲ)络合物的分解过程遵循零级反应模型。多孔硅的热氧化和从二氧化硅表面解吸附2-苯基乙胺(PEA)的过程遵循一级反应模型。
以上讨论了在固态动力学中最常用的反应机理函数的假设和数学推导。对于热分析动力学而言,固态动力学机理函数是具有理论物理意义的,在进行动力学分析时不应仅局限于基于良好的数据拟合得到复杂的数学表达式。
4.5 固态动力学分析中最重要的速率方程
在表4.2中总结列出了广泛应用于固态动力学的速率方程,与此相对应的等温α-t曲线列于图4.9中。这些表达式通常根据等温下的α-t曲线的加速、S形或减速类型进行分类。减速类型可以根据推导过程中所假定的主导控制因素进行细分,主要可以分为几何、扩散或反应级数几种类型。
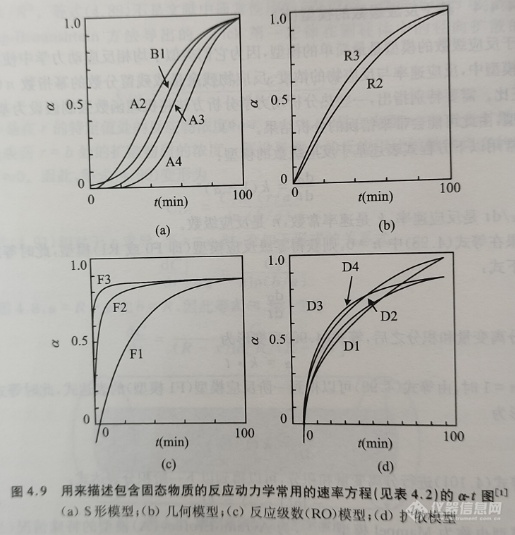
可以用一般形式的速率方程来概括表示表4.2中列出的那些表达式,以下的一个或者两个等式都可以被称为Sest佗k-Berggren方程:
Sest佗k建议将除了(1-α)n之外的其他项都称为“调节系数”,在非均相体系中应用此方程时需要假设它们基于反应级数(Reaction Order,RO)模型来进行修正方程(参见 Koga的研究工作。
4.6等温实验的动力学分析
在进行等温动力学分析时,要求首先对一个已知的恒定温度下被选作研究对象的反应过程进行一系列的(α,t)值的测量。然后对这些数据进行准确分析,以确定表4.2中所列出的方程式中更能精确地反映体系中α随时间变化的最佳方程式。最后,根据得到的比较一致的结果,推导出动力学方程所代表的可以描述反应物/产物界面在反应中按照几何级数发展的方式的模型,并用显微镜观察到的结果来证实这种解释。
对于许多固态反应而言,与α-t数据吻合最好的表达式通常与温度无关,而速率常数的量级随着温度的升高而升高。
4.6.1 反应进度的确定
根据定义,反应进度α随着反应物(开始时α=0.00)到产物(结束时α=1.00)的转变过程而逐渐地发生改变。目前已经有很多实验技术可以用来测量α,主要包括在恒容体系中测量得到的反应逸出的气态产物的压强的改变、反应物的质量变化、逸出气体的分析、部分反应物质的化学和/或X射线衍射测试、热效应的测定等。每种实验技术所测得的参数必须可以定量并且明确地与所关注的反应的进行程度相关,并且其不依赖于其他过程的影响。
如果数据中包括多个速率进程的贡献,则动力学分析的难度就会增加,可靠性会降低。在分步进行的化学变化中,需要分别分析每个独立阶段的化学计量比和动力学。
对于热重实验而言,如果在一个反应中产生一种或者多种气态的产物(逸出气体的组成是常数),则α值可以通过时间t时的质量减少m0-mt和反应完成时的整体的质量损失m0-mf,由α=(m0-mt)/(m0-mf)来计算得到。另外,对于其他技术的测量结果,也可以通过类似的表达式来确定α值。
在需要确定合适的动力学表达式来拟合数据时,准确地测量最终产物的产率非常重要。例如,对于体积收缩(R3)模型(当界面推移到达颗粒中心时,速率过程停止)和一阶(F1)模型(速率持续减小),必须有充分的时间使反应彻底完成。通常通过提高温度来加快反应进程,但这样可能会改变产物分布和/或产生一个后续的反应,另外,测量总反应产物的产率需要与反应的化学计量比相比较。
对于可逆反应而言,使用产物的产率可能会令人产生误解,主要是因为反应是朝着一个平衡进行的,而不是代表已经彻底结束。例如,对于CaCO3的分解反应而言,如果CO2与产物中的CaO发生反应(CaO+CO2→CaCO3),则不能用CO2的生成量来表示正向反应(CaCO3→CaO+CO2)在反应表面的进行程度。利用实验气氛及时带走产生的CO2是一种有效的手段,另外采用较少的样品量和直径较大的坩埚也是使反应朝着正方向进行的有效措施。
在实验中检测到的任何特定的分解产物可能形成于主要的分解步骤或者次要的反应步骤,但是无法在实验中有效地测得以上两个步骤中的α。通常假设由单位质量的反应物得到的气体产物不会随着反应的进程而发生改变。因此,对于包含分解步骤的化学过程而言,确定反应中主要的产物非常重要。
4.6.2 用于动力学分析的实验数据
用于动力学分析的数据必须足够准确并且可以重复,目前尚没有明确的标准来确定这种可重复的行为。通常的做法是在相似的实验中确定和报道α-t曲线,通过使用不同质量的反应物的实验来揭示自加热(自冷却)、逆反应和二次反应的程度和影响,所有的这些过程都会随着固体反应程度的增加而增加。对于反应物的破坏和预处理(例如,预照射、表面磨蚀、老化、研磨、压片、退火等)会明显地改变动力学特性,通过对比未处理和已处理过的反应物样品的反应性可以得到用于描述反应机理的信息。
因此,等温动力学分析的数据由一系列的数值,如α与t、dα/dt与t、dα/dt与α等构成,这些数据之间可以相互转换。在实验时,需要实时记录每个实验的温度。另外,在实验时可能会得到噪音相对较大的α与t、dα/dt与t等数值,在必要的时候可以对数据进行平滑处理。显然,得到的平滑曲线可能会包括一个来自于仪器自身影响的未知贡献。
4.6.3 等温数据动力学分析方法
进行动力学分析的主要目的是从表4.3中找出最适合用来描述每个实验的(α,t)数据的速率方程,对动力学过程进行描述时需要满足以下至少三个方面的要求:
(1)实验值和表4.3中所列公式的α与t、dα/dt 与t、dα/dt与α之间关系的数学拟合结果的准确性。
表4.3 在固态反应动力学分析中最常使用的重要的动力学方程
|
|
|
|
1.加速α-t |
|
|
|
pn 幕级法则 |
|
|
|
E1指数运律 |
|
|
|
2. Sigmoid α-t |
|
|
|
A2 Avrami-Erofeev |
|
|
|
A3 Avrami-Erofeev |
|
|
|
A4 Avrami-Erofeev |
|
|
|
An Avrami-Erofeev |
|
|
|
B1 Prout-Tompkins |
|
|
|
3.减速α-t |
|
|
|
3.1几何模型 |
|
|
|
R2面积收缩 |
|
|
|
R3体积收缩 |
|
|
|
3.2扩散模型 |
|
|
|
D1 |
|
|
|
D2 |
|
|
|
D3 |
|
|
|
D4 Ginstling-Brounshtein |
|
|
|
3.3 反应级数模型 |
|
|
|
F0 |
|
|
|
F1 |
|
|
|
F2 |
|
|
|
F3 |
|
|
|
注:①每一种表达式中的速率常数k是不同的,时间t假设已经进行了诱导期t的校正,
②k的单位通常用min-1来表示。在这些方程式中,指数表达式的形式是α=kn·tn而不是α=k·tn。
(2)可以得到理想的拟合结果的α的有效范围。在一定程度上允许有两个不同的方程应用于一个连续的α范围内,但是首先要阐明单个速率方程并不能代表整个速率过程。
(3)对于这个确定的反应模型而言,必须有其他的实验技术提供互补的、可行的证据,这些技术主要包括光学和电子显微镜、X射线衍射测量、光谱等。
主要采用以下方法来进行等温实验数据的动力学分析:
(1)检查(表4.3中)g(α)时间曲线的线性关系;
(2)对表4.3中由速率方程计算得到的曲线图与α-约化时间图进行比较
这种方法主要通过由一定范围的测量时间值t得到的约化时间值tred,在所有曲线上可以找出一个共同的点。通常当α为0.5时,t0.5=1.0。该情况适用于任何诱导期,所以tred=t/t0.5。
(3)将测量得到的dα/dt-约化时间或α时间图与由表4.3中速率方程给出的曲线相比较。
(4)确定由测量(表4.3)得到的dα/dt值对f(α)图的线性关系。在动力学模型中,通过这种方法比上述的方法(1)可以得到更好的分辨率。
下面将详细介绍这些方法。
在确定可以选用的最合适的速率方程来对一系列的给定数据进行最合理的描述时,需要考虑以下方面的因素:
(1)在不同反应模型的α范围内是最容易区分的;
(2)实验误差的影响,主要包括α测量值的随机分布等。
目前,并没有对于可以认为适合的α范围达成一个普遍的共识。Carter认为,应该将测量值和理论值之间的一致性扩展到几乎完整反应,范围为0.00<α<1.00。实际上,在许多文献报告中仅描述了不同的速率方程在相对有限的α范围内的适用性。因此,在不同的反应阶段可以提出相应的一系列的模型。如果动力学行为的改变可以由如微观观察结果等作为补充证据来支撑这一判断,这种解释的合理性则会显著增加。另外,需注意在将由热分析法产生的平均测量结果与非常有限的部分样品(如表面)的微观细节相关联起来时可能会带来一定的风险,因为这些样品可能会在实验过程中被损坏。例如,样品可能会被电子显微镜的电子束破坏。
4.6.4 g(α)对时间的关系曲线的线性关系的确定
在进行动力学分析时,首先会通过g(α)-时间曲线的线性关系来确定值得更详细考虑的方程。通常在最大的α范围和偏离线性关系的范围之间做出折中处理,最终确定最佳的动力学表达式。对线性关系的偏离可能是由于在反应的开始阶段或最终阶段的测量中的误差造成的。通常采用标准的统计参数来评价定义的α范围的线性程度,这些统计参数主要包括相关系数r、回归得到的直线斜率的标准偏差sb;或者由t、Sxy来确定g(α)的标准偏差,用来量化一组实验点与计算得到的回归直线之间的偏差。在文献中, 已经有不少研究者指出了用r来表示拟合程度的不足之处。当s的值取决于分析中使用的t的范围时,则需要优先考虑使用sb.
通过实验数据和理论方程之间的大小和方向的差异,我们可以用来确定最合适的速率方程和经常采用的残差对时间的曲线图,即(g (α)实验- g (α)预测)-时间曲线。一旦得到了满意的拟合结果,则可以用来确定适用的速率方程g (α)=k·(t-t0)以及在实验温度下的k值,可以由曲线的斜率确定拟合的标准偏差。
对于那些包含指数n的速率表达式,例如,对于Avrami-Erofeev方程而言,通过In[- In(1-α)]对In(t-t0)图可以最方便地确定n的值。然而,通过这样的图得到的结果显然并不一定是最佳的结果,并且有一个关于t0的误差可以显著地影响n的表观值。在文献中已经有了关于分数形式的n值报道。
4.6.5 约化时间和α-约化时间图
可以通过扣除主反应开始阶段的诱导期t0(也包括将反应物加热到温度T的时间)来校正测量时间的值。可以用约化时间因子tred=(t-t0)/(t0.5-t0)的形式来表示实验时间值t-t0,其中,t0.5是当α=0.50时的时间,k·(t0.5-t0)=1.0。
在包括不同的等温温度下的所有实验中,其α-tred测量值都应该落在单条曲线上。这条复合曲线可以与由表4.3中的每个速率方程所计算得到的曲线(见图4.10)进行比较。这样的计算曲线以α=k·tred的形式来进行准确的表示,可以确定每个点的偏差(α理论-a实验)。在将这些差值的数值和其随α的变化情况进行比较后,可以通过动力学数据拟合得到最适合的速率方程和它适用的范围。
在复合曲线的准备过程中,可以识别出随温度变化的α-时间曲线形状的任何系统变化。(tred)-1的大小与温度T时的速率常数成正比,因此,这种方法可以通过约化时间的倒数计算得到活化能来定量测量速率常数k,而不需要确定动力学模型。
4.6.6 在动力学分析中导数(微分)方法的应用
在动力学分析中,可以用足够准确的导数方法来测量或计算出dα/dt的值。在实际的实验中,通过一些如DSC和DTA之类的实验技术可以得到一个与反应速率成正比的输出信号。
动力学分析的导数方法包括dα/dt对α作图法或者dα/dt对tred作图法,可以直接比较实验值与由每个速率方程(表4.3)得到的计算值(图4.10)。第三种求导方法是确认实验测量的速率dα/dt值与表4.3中速率方程的微分机理函数f(α)之间的线性关系。通过这种动力学分析方法可以在现有的动力学表达式中提供更好的区分度,尤其是对于S形曲线所对应的方程(表4.3中的A2到A4)而言,并且其对于几何过程(表4.3中的R2和R3)有很好的应用前景。
4.6.7动力学解释的验证
通过观察,对于得到的由关注的反应的动力学行为符合g (α)=k·t或dα/dt=k·f(α)的结论。对于由一个特定的几何图形的界面推移所引起的动力学行为而言,应尽可能地通过独立的证据来证实这种结果。例如,由方程A3(表4.3)拟合得到的一组(α,t)值可以由瞬时成核之后的核的三维生长过程(η=0,λ=3,因此n=3)引起,也可以由伴随着二维生长(η=1,λ=2,n=3)的线性成核过程引起。作为一种最直接的证实其几何推理的方法,通常通过显微镜观察由部分分解所造成的反应物样品中与界面生长有关的结构变化。
4.7 温度对反应速率的影响
温度对大多数化学反应的速率有很强的控制性影响。这个影响是通过速率常数k的大小来定量进行表达的,通常假设k可以与其他变量进行分离:ate
式中,C是常数,f1(α)是上面讨论过的对反应程度α的依赖性关系。动力学模型函数f1(α)随温度改变的例子是相对少见的,对于温度对反应速率的影响的研究通常是在假设所有其他贡献的影响保持不变的前提下进行的。
通过对很多类型的速率过程进行速率常数的实验测量,结果表明,包括均相和多相的化学反应(以及相关的现象)均符合Arrhenius方程式的一种或其他形式。方程中的参数A和Ea的数值大小代表了一种重要的报道和比较动力学数据的方法。
4.7.1 Arrhenius参数A和Ea的测定
如上所述,通过对等温实验中的数据进行分析,可以得出在每个温度Ti下的一组kt值。这些数值通常以Inki对1/T作图(通常被称为Arrhenius图)的形式得到。通过线性回归可以得到Ea/R和InA的值,以及它们的标准偏差。
c图的线性度,以识别出任何在曲线形状上的变曲
这些数值通常以hki对1/T作图(通常被称为Arrhenius图)的形式得到。通过线性回归可以得到E。/R和lnA的值,以及它们的标准偏差。
在实际的应用中,应该检查Arrhenius图的线性度,以识别出任何在曲线形状上的弯曲或不连续。曲线的任何这样的不连续性发生的温度对于解释反应物的行为都是很重要的。速率常数的表达式也很可能是复合项,其主要包括来自不同速率过程的贡献,这些过程主要有例如成核和生长过程等。k和A的单位应该是(时间)-1。
4.7.2 Arrhenius参数A和Ea的意义
适用于固体反应的Arrhenius参数A和Ea通常与在气体反应碰撞理论中使用的术语一致。活化能通常被认为是发生化学键重组必须克服的阈值或能量势垒, 这是将反应物转化为产物的必要条件。频率因子或者指前项 A 是反映反应情况发生频率的一种度量, 通常被认为是一种包括了反应坐标的振动频率。
反应的 Arrhenius行为已经具有相当成熟的理论基础, 最早被用于均相的速率过程。实际上,该模型在直接应用于固体反应时经常会受到质疑。Garn尤其强调, 在一个具有固定成分的晶态固体中, 能量的分布不能由麦克斯韦-玻尔兹曼函数(Maxwell-Boltzmann 函数)来表述,该函数假设在均匀体系中粒子之间的能量可以自由地进行交换。他认为固体的分解不涉及任何离散的活化状态, 通过对这些反应进行计算所得到的活化能的变化范围很大, 这一现象证实了上述的结论。固体内部的能量在近邻组分间迅速传递, 因此与平均能量并没有显著的区别,这是任何一个可用的活化能模型的基本特征。Bertrand等人定义了Ea为一个复合术语,其主要包括一些对反应的控制有贡献作用的量,例如平衡和热梯度的偏差。
4.7.3 补偿效应
在许多的文献中包含了很多用补偿方程拟合计算得到的固体分解的 Arrhenius参数的报道:
式中,a和b是常数。这种行为模式被称为补偿(compensation),这是因为在出现这一趋势的一组数据内,活化能Ea的增加将会导致反应速率的下降,可通过InA的增加来抵消,这种效应也被称为等动力学效应。因为对一组满足等式(4.106)的(A,Ea)的值而言,存在一个温度TK。在该温度下,所有的速率常数是相等的。对于很多反应而言,Tk的值处于显示补偿行为的动力学测量的温度范围内。
有两类现象通常与动力学补偿效应相关:
(1)一系列密切相关但不完全相同的反应,由类似的实验过程决定Arrhenius参数,并确认满足等式(4.106)。
(2)一系列密切相关但不完全相同的单个化学反应的实验,实验条件的不同主要包括固体反应物的物理状态和热历史,可能会导致表观Arrhenius参数之间呈现等式(4.106)的关系。
尽管已经提出了很多关于补偿行为的理论解释,但是迄今为止还没有一个已经得到普遍认可的合理解释。
4.8 非等温实验的动力学分析
在等温动力学研究中对非等温动力学数据进行分析是为了确定速率方程(表4.3)和用来合理地描述实验结果的Arrhenius参数。在一个典型的非等温动力学实验中,反应物样品所处环境的温度会根据某些特定的程序发生系统的改变(通常但不一定是温度随时间的线性增加)。所有的动力学结论的数值最终取决于由原始测量数据所得到的α、t和T的精度(或者通过微分的方式得到的dα/dt或dα/dT等),其中最重要的是由一个确定的化学计量反应来确定α。在非等温实验过程中,动力学性质的变化可能比一系列的等温实验更容易被忽略。这些可能的变化主要表现在A、Ea和动力学表达式的形式g(α)或者f(α)的变化。另外,反应的化学计量关系、产物的产率和产物的二次反应温度也可能随温度而发生变化。同时,可逆反应、同时反应和连续反应的相对贡献也会随温度的变化而变化。
在相当长的时间内,不少研究者对非等温动力学得到的结果的合理性持怀疑的态度。Boldyreva认为, 对非等温动力学研究的争议主要表现在其温度变化速率与等温研究相比加快了许多。在某些实验条件下,例如在非等温条件下进行的过程中,实验室测量时的反应速率应与实际生产或使用的工艺条件之间的尽可能接近。不能在缺乏更多、更直接的研究结果的情况下,使用非等温动力学方法来确定动力学参数和反应机制。Maciejewski则认为,将得到的动力学参数看做所研究的化合物的特性而不提到在进行动力学分析时所使用的实验条件的做法会带来很大的风险。
理论上,等温和非等温方法是用来确定某一反应的动力学参数的两种互为补充的方法,这两种方法都可以用来解决同一个问题。
等温研究代表了温度变化的众多可能性中的一个极限情况,原则上可以将等温条件下的这些变化应用于非等温研究中。这两种方法都有各自的优点和缺点,在实际应用中不要试图淡化或忽视其中任何一种方法的重要性。
在许多关于非等温动力学的论文中使用了基于反应速率对浓度依赖性的速率方程进行动力学分析(表4.3中F0到F3),这些反应类似于均相反应的行为。通过非等温测量,可以使反应中通常被认为是一个单一的反应过程变为一系列的多个步骤。
如果认为一个固态反应可以发生,那么应该对基于几何模型拟合得到的数据进行合理的评价,通过适当的其他互补的技术手段如显微镜技术等尽可能地加以证实所得到的结论。
4.8.1 实验方法
最常见的实验方法是在合适的恒定加热速率β的条件下完成的,大多数的商品化的仪器均可以满足这种方法,在实际上也可以采用以下的温度-时间变化方式:
(1)恒定反应速率热分析(Constant Rate Thermal Analysis,CRTA)技术。通过该技术使样品以特定的方式进行加热,使反应以恒定的速率发生。用该方法来控制温度,使反应以不断增加的速率(即加速度)进行。
(2)温度跳跃式或步阶式的温度控制程序。在单次的实验中,温度迅速发生变化(即“跳跃”),从一个值快速地达到另一个值,可以通过测量得到两个(或更多的)温度下的变化速率,用来计算在特定的α值时的Arrhenius参数。该方法假定在测量两个速率值的时间内,α不会发生显著的变化。
(3)温度调制程序,这种技术常用于区别对由热行为和动力学因素所引起样品的程序温度随时间发生小的周期性的振荡变化,可用于区分可逆和不可逆的贡献。
在进行温度校准时,测量的温度和校正的样品温度之间的差异有时可能会很大。Agrawal建议至少在70K的温度变化范围内来评价Arrhenius参数。
尽管通常将实验方法划分为等温动力学和非等温动力学分析方法两种方法,然而,在实际上由所选用的其他类型的实验条件所得到的真实的样品温度为近似值。在实验过程中,从加热炉到样品之间的热传递、样品在反应期间复杂的自冷却或自加热现象、滞留在样品附近的气体产物对可逆反应的影响等因素对非等温实验条件的影响。在对等温实验结果进行动力学分析的过程中,也会遇到一些问题。例如,经常会遇到如何将得到的数据在尽可能广的α范围内进行数据拟合,以及如何区分相似形式的动力学表达式等问题,在程序控制温度的条件下这些问题会变得更加复杂。无论温度程序如何变化,在研究化学反应、相变和结构变化等过程中的动力学过程时,都应该从其他相关分析方法和微观证据中获得有效的支持。
4.8.2 理论热分析曲线的形状
表4.3中列出了在等温条件下的各种动力学模型在理论上的α-t表达式,每种模型所对应的曲线形状如图4.10所示。即使是在等温条件下,通常也很难正确地区分这些模型。在非等温过程中,即在线性程序控制温度的条件下,这些曲线的形状发生了相当大的改变,各种模型的理论α-T曲线如图4.11中(a)、(b)和(c)所示。这些曲线是通过Doyle近似来计算温度积分p(x)得到的。图4.11(b)为根据反应的表观化学反应级数n(n也包括分数值)的动力学反应模型,即F1、F2、F3、R2和R3所得到的分析结果。由图可见,对于低α值的反应而言,很难直接进行区分。在较高的α取值范围内,由图可以有效地分辨出较高级数的反应。根据扩散模型,即D1、D2、D3和D4,可以得到的起始温度比基于n级反应模型假设的更低,曲线形状也更为扁平(即由延长的温度间距所引起)(见图4.11(c))。然而,根据Avrami-Erofeev(JMAEK)模型,即An(见图4.11(a)),则可以得到具有较高的起始温度和更陡的曲线。图4.12中(a)、(b)和(c)给出了与由图4.11中所示的积分曲线得到的相对应的微分曲线。
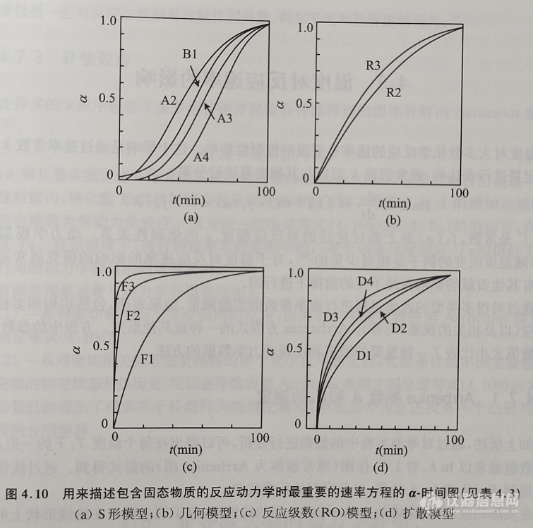


对于一个固定的模型而言,例如R3模型,其他变量例如加热速率β、指前因子A和活化能Ea的影响分别如图4.13~图4.15所示。Elder通过动力学模型得到了类似的曲线,Zsak佼的研究结果表明,对一阶(F1)模型而言也有类似的影响。虽然F1模型并不是一个非常真实的表达形式,但它通常被假定为一个近似形式来进行应用。图4.8显示了在β=1~16K·min-1的加热速率范围内,加热速率以成倍地增加对理论的R3曲线所产生的影响。在A=1017~1013s-1的范围内,其以数量级的形式降低,指前因子主要会影响曲线的起始温度和加速部分(见图4.9),其余部分则几乎平行。如果按照5kJ·mol-1的间隔增加活化能,也可以得到与此非常相似的结果,如图4.15所示。


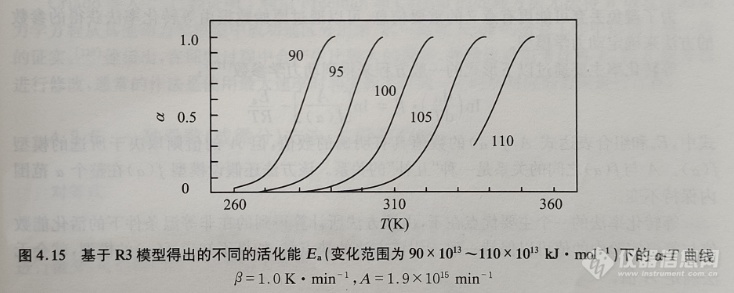
因此,热分析曲线(α,T)的整体形状主要由动力学模型决定,而曲线在温度轴上的位置则是由Ea、A、较低的反应程度α和升温速率β来决定的。
4.8.3 非等温动力学方法的分类
用于分析非等温动力学数据的方法可以分为基于等式(4.7)的导数或微分方法(该方法为ICTAC推荐首选的方法)或者是基于等式(4.9)的积分方法。
Vyazovkin和Lesnikovich对这种传统的分类方法提出了异议,原因是这些分类方法特指的是使用的实验数据的类型。他们建议使用一种基于动力学参数计算方法的分类方法,该方法包括“可识别法”(即可以识别动力学模型f(α)或g(α))和“非识别法”。
可以将涉及可识别的方法进一步细分为两种:一种是可以称为“分析”的方法,该方法主要用一个模型来描述实验数据;另一种则是可以称为“合成”的方法,该方法结合几个模型来更好地描述数据。进一步的子分类可以基于对动力学表达式的控制,使其适合于用线性回归的方法来测试所得到的拟合数据的质量,通常较少使用非线性回归的方法。
如果对速率表达式的形式做出假设,则只能从单次的动态(α-T)的实验数据对反应过程中的3个(或者更多)未知特征量A、Ea和机理函数f(α)或g(α)进行估算。许多研究者在不加合理判断的前提下,直接地将所研究的反应看做一个一级反应(F1)的过程[即f(α)=(1-α)和g(α)=-ln(1-a)]。
尽管已经提出了将动态实验和等温实验相结合的方法,比较常见的是在不同的加热速率下从两次或两次以上完全相同的动态实验中计算出动力学参数,但由于不同加热速率的实验条件可以导致样品中不同的温度梯度,因此在这种情况下如果不对温度进行校正,仍然可能会得到错误的动力学结论。
4.8.4 等转化率法
当有超过一组的实验结果可用时,通过比较在两组不同条件下的一个相同值α下所得到的测量值,可以消除机理函数f(α)或g(α)的未知形式的影响。因此,这些等转化率的方法是一种通过“不依赖于模型”或“非识别”的方法来确定Arrhenius参数的一种技术。这些方法最近由Vyazovkin 和Lesnikovich做了进一步的发展。
为了避免丢弃可能更有意义的重要信息,可以通过原始数据由等转化率法获得的参数的方法来确定动力学模型。
等转化率主要通过以下形式的一般方程来得到动力学参数:
式中,Ea和组合表达式 A/f(α)的数值具有明确的数值,但A的值则取决于所选的模型f(α)、A与f(α)之间的关系是一种“互补”的关系、该方法还假设模型f(α)在整个α范围内保持不变。
等转化率法的一个主要优点在于,由该方法所计算得到的在非等温条件下的活化能数值与等温实验中的值可以保持一致,该方法的缺点是,如果不知道f(α)的模型,就会无法确定A值。
4.8.5 一种导数(或微分)方法:一阶导数法
这些方法是基于等式(4.7)进行变换得到的,这类方法可以表示成为多种形式,例如:
如果假设了f(α)的表达式形式,那么可以通过y对1/T曲线的斜率和截距来确定Ea和A的值。由于等式(4.107)左侧的灵敏度与dα/dt成反比,因此除非使用了适当的加权因子,否则得到的动力学参数对热分析曲线的初始阶段和终止阶段的数据非常敏感。在dα/dt最大值附近区域的灵敏度降低,大部分反应都是在该处进行的。
如果有几组数据可用,例如在不同的加热速率βi下进行一系列的热分析实验,则可以应用不同的数学方法来进行分析。
Friedman方法通过In(dα/dt)对1/Ti作图,得到在不同加热速率下(或不同的恒温反应温度,Ti)α相同的值。通过所得到的In(dα/dt)对1/Ti的曲线,可以得到一组在不同转化率下的平行线。其斜率为-Ea/R,截距为ln[A·f(α)i]。每条线的斜率相同,而截距则各不相同。通过将得到的截距对αi外推至αi=0,可以得到A的值。
Carroll和Manche所提出的方法与上述Friedman方法的处理过程十分相似,区别在于该方法需要通过ln[β·(dα/dT)]对1/T作图。
Flynn对这一方法做了进一步的改进,改进后的方法是在不同的加热速率下,首先得到不同的加热速率下相同的转化率αi对应的Ti,然后通过Ti·ln(dα/dt)i对Ti进行作图。通过这种方式得到的直线的截距都相同,为-Ea/R,但是斜率不同,为In[A·f(α)i]。
被广泛使用的Freeman和Carroll方法,假设反应满足f(α)=(1-α) ′′的形式,并考虑以(dα/dT)、(1-α)和1/T表达增加的差异变化,可以导出下列形式的表达式:
通过上述形式的表达式,采用以下两种方法中的任一种进行作图,根据斜率来确定Ea的值: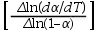 对
对 作图法或者
作图法或者 对
对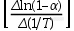 作图法。
作图法。
Criado等人已经证明了利用Freeman和Carroll的处理方法无法将n级反应的动力学方程从其他动力学模型中成功地区分出来,这一点在Jerez的研究工作中得到了进一步的证实。他指出,在回归过程中会产生比较大的误差,并建议对用来计算Ea和n的方法进行修改,通常的作法是使用最大速率时和实验进行到一半时所对应的数据进行计算。
4.8.6一种导数(或微分)方法:二阶导数法
对等式
进行微分,可以得到以下形式的关系式:
由于在TG曲线的拐点或DSC峰值的最大值点上所得到的这个导数必须为零,因此存在如下的关系式:
如果n和Tp已知,可以通过实验曲线确定(dα/dT)p和αp,则可以由上式计算出Ea的值。
联立等式(4.109)和等式(4.110),可以得到下式:
由于(1-αp)是在给定的n值下所得的常数,因此可以用Kissinger方法来获得Ea的值。
假设反应机理函数为f(α)=(1-α)n,由等式(4.7)可以得到以下的相应形式的动力学方程:
该方程可以用来与一条相应的热分析曲线得到的转化率-温度曲线相对应,对方程(4.112)两边微分,可得
在热分析曲线的峰顶处,其一阶导数为零,即边界条件为
将上述边界条件代入等式(4.113),可得
式中, 与β无关,其值近似等于1。因此,等式(4.116)可变换为
与β无关,其值近似等于1。因此,等式(4.116)可变换为
对等式(4.117)两边取对数,可得等式(4.118),也即Kissinger方程:
方程(4.118)表明, 与
与 呈线性关系,将二者作图可以得到一条直线,从直线斜率求Ea,从截距求A,其线性相关性一般在0.9以上。
呈线性关系,将二者作图可以得到一条直线,从直线斜率求Ea,从截距求A,其线性相关性一般在0.9以上。
在不同的加热速率βi下进行实验得到实验曲线,通过不同的加热速率βi的曲线用 对
对 进行作图,所得到的曲线的斜率是-Ea/R。
进行作图,所得到的曲线的斜率是-Ea/R。
Augis和Bennett 用适用于许多固态反应的Avrami-Erofeev(或JMAEK)模型(An,表4.3)对Kissinger方法进行了修正,他们用In[β/(Tp-T0)]对1/Tp(T0为在加热程序开始时的初始温度)进行作图,而不是使用 对1/Tp进行作图。Elder将 Kissinger方法进行了推广,使其可以应用于所有的动力学模型,该广义方程可以用下式表示:
对1/Tp进行作图。Elder将 Kissinger方法进行了推广,使其可以应用于所有的动力学模型,该广义方程可以用下式表示:
式中,m为修正后的Arrhenius方程中指前项中的温度指数,通常取值为0,L=-f(αp)/(1+mRTp/Ea)。
虽然这个修正项值通常相对较小,但通过它有助于区分相似的模型。
虽然Ozawa处理方法最初是作为一种积分的方法发展起来的,但它也适用于类似于Kissinger法可以处理的导数曲线。
由等式(4.9)求积分,可得下式:
式中
对p(u)的不同处理,构成了一系列的积分法方程,其中最著名的方法为Ozawa法。
通过对等式(4.120)进行变换,可以得到下列形式的Ozawa方程:
可用以下方法求得等式(4.123)中的Ea:
由于不同βi下各热分析曲线的峰顶温度Tpi处各a值近似相等,因此可用“lgβ-1/T”所呈的线性关系来确定Ea值,使得
这样由式(4.123)可以得到以下形式的线性方程组:
解此方程组可以求得a值,从而可以求得Ea值。
Ozawa法有效地避开了反应机理函数的选择而直接求出Ea值,与其他方法相比,它避免了因反应机理函数的假设不同而可能带来的误差。因此往往被其他学者用来检验由他们假设反应机理函数的方法求出的活化能值,这是Ozawa法的一个突出优点。
在Ozawa方法中,以Inβ对1/Tp进行作图,所得到的曲线的斜率是-Ea/R。VanDooren和Muller的研究结果表明,通过使用Kissinger方法和Ozawa方法由DSC实验确定的表观的动力学参数时,样品的质量和颗粒尺寸都会对动力学参数的数值产生不同程度的影响。通过这两种方法均可以得到类似的值,但Kissinger方法的精度稍低一些。建议使用α=0.5(即转化考虑为一半时)时所对应的温度,而不应该使用Tp的数值。
Borchardt-Daniels方法最初是在使用 DTA 法研究均相的液相反应的基础上发展起来的,可以通过以下表达式来计算速率常数k;
在上述的速率常数的表达式中,V为样品的体积,m0为用摩尔数表示的初始样品量,S为DTA峰的面积,s为时间t时的DTA峰的部分面积,峰值高度ΔT和斜率dΔT/dt的测量均可以由DTA曲线测量得到。J为热传递系数,C为样品和支持器的总热容。实际上,J和C的数值无法准确获得,通常假设n=1。由于C · (dΔT/dt)和C·ΔT相对于与其相加的项(或者与其相减的项)比较小,可以近似为0。因此,速率常数可以简化为以下形式:
对于DSC曲线而言,其等价形式的表达式可以用下式表示:
式中,H为焓,dH/dt是DSC信号。得到的k值用在常规的Arrhenius图中。
另一种基于二阶导数的方法是Flynn方法和Wall方法。
对于下式:
假设b2=d1=d3=0,对等式(4.128)重新排列,可以得到以下等式:
将上式对α进行微分,可以得到
当α的值较小时,以上等式(4.130)中的右边的最后一项可以忽略不计。由于2T«Ea/R,故有时甚至会将2T这一项忽略不计。如果使用有限的差分来替代导数形式的表达式,则可以得到以下表达式:
在等式(4.131)中,Tave为反应区间内的平均温度。在反应的早期阶段,可以通过(T2(dα/dT))对Δα的曲线的斜率计算出Ea的值。
4.8.7 形状因子法

M佗lek在热分析(TA)曲线的动力学分析中,将早期的Kissinger模型进行了扩展,引入了“形状因子”(shape index,通常用S表示)的概念。S被定义为在曲线的上升和下降拐点区域的切线的斜率的绝对值的比值,切线的斜率由热分析曲线的峰值来确定(见图4.16),即
在拐点处,S值和温度T1和T2的值是很容易确定的。计算用S值表示的理论速率方程取决于温度积分函数p(x)的表达式。如果选择了一个合适的p(x)的近似表达式,则可以得到一个可用于所有的具有两个拐点动力学模型的S和T1/T2的比值之间的线性关系(参见表4.3)。
4.8.8导数(或微分)方法和积分方法的对比
在动力学分析中,使用微分法可以有效地避免在积分法中所必需的温度积分的近似(如上所述)问题。另外,在使用微分法时的测量也不受累积误差的影响,而且在计算过程中也不会出现在进行积分时难以确定的边界条件。对以积分方式测量的数值进行微分时,通常需要在进一步分析前对数据进行平滑。在确定动力学模型时,使用微分方法可能会更加灵敏。但是,在进行平滑时可能会导致曲线变形。
4.8.9非线性回归方法(non-linear regression methods)
绝大多数的非等温动力学方法都涉及对速率方程进行适当的线性化处理问题,通常会进行一个对数变换来实现,由此会导致误差的高斯分布发生变形。因此,通常采用非线性方法来避免这一现象。
Militkŷ、Scst佗k和Madar佗sz等人-概述了按照以下形式的关系式进行非线性回归的常规做法:
式中
式中,Aj的值经优化后可以得到如下式所示的最小值的形式:
在确定实验值与理论数据之间的重合程度时,必须考虑在确定最小偏差时的具体情况。然而,由于Ea与A之间的补偿关系,最小值通常会出现“平坑”(flat pit)的现象,而且也有可能会找到一个局部的而不是一个整个范围内的最小值。因此,通常通过一种寻找最小值的方法来确定最小值,该方法考虑到了每个参数对理论曲线的影响。
4.8.10 动力学行为的预测
动力学研究的一个主要目的是可以用来预测不仅仅局限于原始实验测量条件下的动力学行为。预测结果的可靠性依赖于动力学参数A、Ea和α(或Ea)的数值,这些数值不随温度T的变化,并且其精确度已知。可以由下式求得时间的相对误差Δt/t:
计算结果可以用下式表示:
Flynn回顾了由相对较高的温度下获得的分解参数对较低温度下聚合物使用寿命进行预测的方法,并讨论了在使用这些方法的过程中得到错误结果的原因,其中包括了外推超过相变(同时物理性质发生变化)发生的温度的因素。
4.8.11 动力学标准方法
Gallagher列举了可用于进行反应速率对比的动力学标准方法,其对反应的主要要求为:
(1)仅具有单一步骤的不可逆的基元反应。
(2)具有较低的焓值,自加热或自冷却效应尽可能小。
(3)有足够宽的温度范围, 以确保反应在可观测的前提下尽可能缓慢地进行, 注意此处所指的反应缓慢进行并不是说反应越慢越好,否则会带来温度测量的误差。
(4)样品与实验气氛之间不发生反应。
(5)反应不随样品的制备方法、预处理过程和样品粒径及其分布的改变而发生变化;
(6)由反应过程引起的待测量如质量、逸出气体的量或焓变等的变化应足够明显,在此前提下可以使用少量的样品。换言之,测量仪器应对这些变化足够敏感,以满足微量反应的要求。
对于以上的这些要求而言,有的要求彼此之间并不兼容,因此必须选择出一个折中的方案。
4.9总 结
针对动力学分析的非等温方法和等温方法的相对值而展开的讨论通常会不了了之。一方面,有的体系在非等温和等温的实验条件下可以得出较为一致的动力学研究结果;而另一方面,也存在着一些体系的动力学分析结果强烈依赖于所采取的实验方法,通过不同方法得到的动力学分析结果之间的差别较大。因此,通过这两种途径的互补,在发现如上文所述的潜在的误差来源时很有意义。通过等温和非等温这两种技术都可以针对所发生的过程提供有价值的信息,使实验者充分理解每一种方法的缺点和限制。由等温数据得到的动力学参数不受所选择的动力学模型的明显影响,而非等温过程则相反。原因在于在分析时通过等温测量确定Arrhenius参数,而通过非等温测量确定动力学模型。
很多情况下,使用相同的实验数据,利用不同的数学分析方法,却可以得到结果明显不一致的动力学参数,这种现象使人感到十分迷惑。在某些可用于动力学分析的商用软件程序中甚至没有明确指出其所依据的具体算法,而其他的动力学分析软件包则大多使用仅限于反应级数(RO)模型的动力学表达式。
Ninan在一篇论文中概述了动力学的这种复杂性,他认为:“在等温和非等温之间,以及模式匹配和非模式法之间存在着旷日持久的争论。至少在我们的研究中,我们没能找到其中一方绝对优于另一方的证据;二者中的任何一方均拥有各自的优点和缺点。热分解反应的机理不能单从对TG数据的数学拟合曲线中得到不容置疑的结论,而通过等温下的质量损失数据可以给出更深层次的反应机理信息。至于所关心的动力学参数的数值,从表现出相同程度波动和变化趋势的角度来说,在等温和非等温、模式匹配和非模式法之间并不存在着明显的差别,对于这个问题需要结合具体的问题进行具体的分析。因此,如果我们以计算动力学常数为目的,非等温方法具有更加简便的优势。然而,在提出某固态热分解反应的机理和得到其动力学信息的结论之前,我们必须要明确过程中实验条件的因素对动力学参数的影响。最后,在了解过程中每个可能因素的影响之后,我们才有可能通过动力学分析来预测动力学参数,从而获得一整套实验参数的设想是可行的。

















 。
。
 定义的转换分数。因此,α′≥α。我们可以通过与α′值的关系来评价α的值。
定义的转换分数。因此,α′≥α。我们可以通过与α′值的关系来评价α的值。











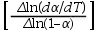 对
对 作图法或者
作图法或者 对
对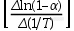 作图法。
作图法。 与β无关,其值近似等于1。因此,等式(4.116)可变换为
与β无关,其值近似等于1。因此,等式(4.116)可变换为 与
与 呈线性关系,将二者作图可以得到一条直线,从直线斜率求E
呈线性关系,将二者作图可以得到一条直线,从直线斜率求E 对
对 进行作图,所得到的曲线的斜率是-E
进行作图,所得到的曲线的斜率是-E 对1/T
对1/T
