小弟求助各位大哥,我2月24日就要考试计量认证了,但是还没搞懂复习资料上的,希望大家帮帮我。3个计算:合成标准不确定度,有效自由度,扩展不确定度的公式及原理与计算e-mail:yangjun19821112@sina.comQQ82633178十万火急!!!!!
在看一些大咖写的测量不确定度的书,一上来就祭出量子力学的大旗,大谈量子力学中测不准原理,想给测量不确定度弄个高大上的出身;但是很可惜,测量不确定度其实是数理统计中的区间估计原理在测量中的应用,测不准原理是阐述粒子的波粒二象性的,两者毛关系都没有。[b][color=#ff0000]别人可以瞎说,但是咱们不能轻信。[/color][/b]
[color=#0166a9]为了评定测量结果的质量如何,要用测量不确定度来描述。ISO/IEC导则25指明实验室的每个证书或报告,必须包含有关评定校准或测试结果不确定度的说明,当我们给出测量结果时,应根据需要给出测量不确定度。本文从历史的角度简单介绍从测不准原理到测量不确定度的使用过程。[/color][color=#0166a9] 1927年,德国物理学家海森堡(HeisenbergWerner,1901—1976)提出了测不准关系,即测量一个微粒的位置时,如果不确定范围是ΔX,同时得出其动量也有一个不确定范围ΔP,那么ΔP和ΔX的乘积总是大于一定的数值,表示为ΔPΔX≥h/2。[/color][color=#0166a9] 这里h=h/2π,h为普朗克常数,等于6.626×10[sup]-34[/sup]焦耳秒。[/color][color=#0166a9] 这个测不准关系表明,如果要对物体的动量进行非常精密地测定,即ΔP→0,那么位置就非常不确定,即ΔX→∞。反之,要位置精密测定,动量就非常不确定。[/color]

GUM法评定不确定度时认为:分析结果符合正态分布,依据各个分量通过测试模型来计算得到分析结果;利用方差传播定理和测试模型来计算分析结果的标准差s;通过各分量不确定度和自由度计算分析结果分布的自由度n,然后在给定的置信概率下,确定包含因子K,最后按照要求把评定结果表示出。 http://ng1.17img.cn/bbsfiles/images/2016/08/201608221012_606083_1898299_3.png可以参考这个ppt,不明白的去学学数理统计,包含因子,扩展不确定度等就都弄清楚了。
请教大家,针对蓝色字体内容,是否有一些案例说明?哪些检测方法难以评估不确定度?一般方法不是只给出精密度数据很少会给出不确定度吧?7.6.3 开展检测的实验室应评定测量不确定度。[color=#3333ff]当由于检测方法的原因难以严格 评定测量不确定度时,实验室应基于对理论原理的理解或使用该方法的实践经验进行评估[/color]。注 1:某些情况下,公认的检测方法对测量不确定度主要来源规定了限值, 并规定了计算结果的表示方式,实验室只要遵守检测方法和报告要求,即满足 7.6.3 条款的要求。 注 2:[color=#3333ff]对一特定方法,如果已确定并验证了结果的测量不确定度,实验室只 要证明已识别的关键影响因素受控,则不需要对每个结果评定测量不确定度[/color]。
测量不确定度来源的识别应从分析测量过程入手,即对测量方法、测量系统和测量程序作详细研究,为此必要时应尽可能画出测量系统原理或测量方法的方框图和测量流程图。检测和校准结果不确定度可能来自;(1)对被测量的定义不完善;(2)实现被测量的定义的方法不理想;(3)取样的代表性不够,即被测量的样本不能代表所定义的被测量;(4)对测量过程受环境影响的认识不全,或对环境条件的测量与控制不完善;(5)对模拟仪器的读数存在人为偏移;(6)测量仪器的计量性能(如最大允许误差、灵敏度、鉴别力、分辨力、死区及稳定性等)的局限性,即导致仪器的不确定度;(7)赋予计量标准的值或标准物质的值不准确;(8)引用的常数和其他参量不准确;(9)测量方法和测量程序中的近似性和假定性;(10)相同条件下,被测量重复观测的变化。测量不确定度的来源必须根据实际测量情况进行具体分析。有些不确定度来源可能无法从上述分析中发现,只能通过实验室间比对或采用不同的测量程序才能识别。在某些检测领域,特别是化学样品分析,不确定度来源不易识别和量化,测量不确定度只与特定的检测方法有关。分析时,除了定义的不确定度外,可从测量仪器、测量环境、测量人员、测量方法等方面全面考虑,特别要注意对测量结果的影响较大的不确定度来源,应尽量做到不遗漏、不重复。
摘要: 目的 建立并运用火焰原子吸收分光光度法测定工作场所空气中钴的不确定度评定方法。方法 依据JJF1059.1-2012《测量不确定度评定与表示》原理和方法分析测定过程中不确定的来源,识别其中的主要来源。结果 工作场所空气中钴含量为(0.0453file:///C:\DOCUME~1\ADMINI~1\LOCALS~1\Temp\ksohtml\wpsF0.tmp.png0.0298)mg/m3,K=2。其不确定度主要来源于采样的引入、标准溶液的配制、工作曲线的拟合、样品前处理、样品重复测定及原子吸收分光光度计。结论 运用本不确定度评定方法对测定过程中关键环节的识别,将有助于检测人员重点关注关键环节的质量控制,更有效地提高检测工作的质量。1 原理与方法1.1 评定项目1.2 原理 空气中气溶胶态钴及其化合物用微孔滤膜进行采集后,加消化液(高氯酸:硝酸=1:9)在电热钢板200℃消解后,在240.7nm 波长下,用乙炔-空气火焰原子吸收光谱法测定。1.3 仪器与试剂1.4 方法按照GBZ/T160.8-2004的方法进行测定。2 数学模型3 测量不确定来源的分析 空气样品中钴浓度的测量不确定因素主要包括:①采样器、温度和气压引起采样体积误差的不确定度分量u1;②标准储备液和配制标准溶液时所用的容量瓶、吸管等引起的不确定度分量u2;③样品重复测定产生的不确定度分量u3;④样品消解时产生的不确定度分量u4;⑤工作曲线拟合带来的不确定度分量u5;⑥原子吸收分光光度计测定样品的不确定度分量u6。4 标准不确定度的评定4.1采样器、温度和气压引起采样体积误差的不确定度分量u14.2 标准储备液和配制标准溶液时所用的容量瓶、吸管引起的不确定度分量u24.2.1 标准储备液的相对标准不确定度u(2,1)4.2.2 标准溶液的配制u(2,2)4.3 样品重复测定产生的不确定度分量u34.4 样品消解时产生的不确定度分量u4 4.5 工作曲线拟合带来的不确定度分量u54.6 原子吸收分光光度计测定样品的不确定度分量u65 合成相对标准不确定度ux相对标准不确定度分量一览表相对标准不确定度ux 相对不确定度来源 相对不确定度值u1 采样引起的不确定度 0.012U2 配制标准溶液引起不确定度 0.017U3 样品重复测定产生不确定度 0.0023U4 样品消解时产生的不确定度 0.0023U5 工作曲线拟合的不确定度 0.33U6 仪器本身引入的不确定度 7 结论 空气样品中钴浓度为0.0453mg/m3,钴的职业接触限值为0.05mg/m3,从数据看会判定为合格,通过对空气样品中钴浓度的不确定度分量的分析和计算,可以看出测定结果有超出接触限值的可能,这样评价人员能更准确判别是否存在职业病危害因素,来提出更合理的改善方案。从表2可以看出曲线拟合所产生的不确定度为最主要因数,由此,我们更要注意测定过程中的各个方面,减少误差,降低不确定度,以保证实验数据的准确性。
真值、误差、准确度,是误差理论的核心概念。不确定度论的立足点是否定真值,从而否定误差、否定准确度。这是很自然也是很明白的事,不否定真值,不确定度就没有存在的理由。否定真值有两个层次:一是否定真值的存在,一是否定真值的可知性。VIM第一版写到“量子效应排除唯一真值的存在”,这是说真值不存在。在“不确定度理论置疑”一文的网上讨论中,已找到何祚庥院士“测不准关系正释”一文,又找到哥伦比亚大百科全书中所载的不确定性原理的提出者海森堡的原话。上述两篇文章都说明量子理论的不确定性原理(我国旧译测不准关系),不限制单一量测量时的测量准确度,因此说“量子效应排除唯一真值的存在”,是对量子理论的误解,是错误的。VIM以后各版及GUM不说真值不存在了,而说真值不可知。于是,真值不可知的论调成了不确定度论的主调。这种论调是错误的。现为真值正名如下。-1 真值的真理测量的目的是确定真值。由于测量仪器的限制,得到的是测得值。测得值与真值之差是误差。人们用测得值与误差范围来表征真值。依误差大小,可把量值分为测得值、相对真值、真值。通常测量结果是测得值。各级计量标准的值是相对真值,人类认识到的最高的相对真值是约定真值。误差无限小、相对真值的极限是真值。初看,真值和真理可相比拟;细想,真值是真理的一种形态,真理涵盖真值的道理。真值就是客观值、实际值、准确值。测量讲究准确,追求准确。真值就是准确值。准确分相对准确和绝对准确。相对准确值是有误差的值,是具体条件下对量的正确认识。绝对准确寓于相对准确之中,相对准确包含绝对准确的因素。随着误差逐渐减小,相对准确越来越接近绝对准确。误差无限小时,相对准确的极限是绝对准确。真值的表征值是相对准确的相对真值。-2 真值的数学表达真值,可用数学的语言表达如下。测量计量依准确度的高低而分等级,通常1级高而2级低,此处为叙述方便,倒过来,按楼层的排法,1层低而2层高,这类似医院等级的分法。日常用的测量仪器叫1层,高一档的叫2层,依此类推。设被测量L的真值为Z,各层次的测得值为数列L(N),N从1到N。测量的误差范围(可用误差方程算出误差范围)为δ=| L(N)- Z|, 任给正小量ε,提高测量准确度的层次,可使δε,则Z是L(N)的极限。即真值是误差逐级减小时测得值数列的极限。
本文介绍紫外能谱仪的作用原理及仪器波长值的标定方法,对定值中的误差源进行分析,针对具体仪器推导出不确定度计算公式,通过对公式中各变量的分析,分别计算各变量引起的不确定度,最后给出扩展不确定度及分析结果。
求助一下两个问题:1、相对不确定度,扩展不确定度,标准不确定度,请问以上几个不确定度到底是什么关系???2、在合成部确定度的时候用的是哪个不确定度?新手,刚接触,看的云里雾里。
猫在做一个用GC/MS测塑料中VOC含量的不确定度评定原理是:在一条校准曲线上读出样品的峰面积,然后得到样品某项VOC浓度含量在涉及GC/MS所引入的不确定度分量中,由此台设备引入的不确定度分量按理说是应该看校准证书,可校准证书给出了一堆以下信息:---------------------质量准确性(u):0.1分辨力R(u):0.60测量重复性(%):3.09--------------------以上的信息哪个是要考虑到不确定度分量的影响因素呀?各位大神知道吗?

据国外媒体报道,宇宙理论学家发现我们的宇宙需要“不确定性原理”存在,量子力学的框架似乎不像过去所认为的是完全凭借直觉或者感觉来感知,并将切实体现在宇宙理论之中。如果我们将“不确定性原理”剔除出我们的宇宙,那么我们可能会得到一台“永动机”,这意味着我们的宇宙就是一台名副其实的超级永动机。这些发现已经使得许多物理学家感到不安,因为他们无法打破常规思维去理解这些怪异的量理论,其中就包括阿尔伯特·爱因斯坦(Albert Einstein)。爱因斯坦此前认为宇宙不存在“不确定性原理” 量子力学在20世纪初由一群顶尖的物理学家创建,将人们带入了另一个神奇的世界,我们通过这个理论可以解释和预测出各种无法用经典物理学解释的现象,并且在当今世界科技中也处处体现出量子力学的存在,但是量子力学的世界确实一个违法经典直觉的大集合。其中之一就是“不确定性原理”,该原理由德国物理学家海森堡提出,说明了在量子力学体系中,我们不可能同时获得一个粒子的位置和动量信息。也就是说,我们如果对其中一个粒子位置参数测量得越精确,那么对另外一个动量参数就测得越不准确,我们不可能同时得到两者的精确信息。 对于海森堡的“不确定性原理”,我们可以用一个著名的双缝干涉实验进行说明。由光源发射出的光子在经过双缝时可产生干涉图像,并在后面的屏上显现出来,我们现在将一个光子探测器放置于其中一个双缝处,对通过的光子进行测量,如果我们探测到光子的动量信息,也就是速度的大小,那么我们对光子的位置判断将越来越“模糊”,以至于在屏幕上的干涉图像变得无法识别。http://ng1.17img.cn/bbsfiles/images/2012/07/201207030913_375469_2518341_3.jpg著名的双缝干涉实验 不过,一些科学家认为海森堡提出的“不确定性原理”是无法接受的,而真正原因并不是人们缺乏相关知识而无法理解,而是这个物理法则体现出的思想不能被一些宇宙物理学家接受。比如,对“不确定性原理”持有较大异意的就是阿尔伯特·爱因斯坦,他认为“不确定性原理”不可能成为宇宙物理的基本法则之一,并与另外两名科学家提出了著名的EPR悖论,认为依据“不确定性原理”对相隔遥远的两个粒子系统进行测量将导致超光速现象出现。 根据英国牛津大学的物理学家奥斯卡·达赫斯塔(Oscar Dahlsten)认为,许多人仍然凭直觉认为“不确定性原理”不应该存在于宇宙中。在此前,研究人员提出了一个全新的概念来解释量子力学中出现的诡异问题,如“隐变量”被认为可能是量子力学的幕后操纵者,使得在量子力学体系中的物体变得更加离奇古怪。但是到目前为止,该方法已经失败了。现在,来自新加坡国立大学量子技术科学研究中心的研究人员斯蒂芬妮·韦纳(Stephanie Wehner)和易斯特·翰吉(Esther Hänggi)提出了一种新的解决方法,通过信息理论的语言来重塑“不确定性原理”。http://ng1.17img.cn/bbsfiles/images/2012/07/201207030914_375471_2518341_3.jpg量子力学的世界将是非常怪异和神奇的 首先,他们认为一个单一测量对象的两个属性信息不可能被同时精确地获得,这就如同对同一个测量粒子赋予两种不同的信息编码,同样我们不可能通过任意一种精确的方式或者精度水平去了解这个粒子的动量和位置信息,如果用信息理论语言表达的话,那就是我们不能将两种不同的信息编码解开。如果我们对第一条信息了解得越精确,那么我们对第二条信息的解读能力将受到更多地限制。 接下来将是假设性的计算过程,如果物理学家们放宽“不确定性原理”的各种限制因素,在这种情况下允许信息被更好地解读,并让我们获得在“不确定性原理”法则中规定不允许被获得的信息。在这样的假设前提下,研究人员斯蒂芬妮·韦纳和易斯特·翰吉的研究结果显示,在一个系统中将会存在“无中生有”的能量,系统输出的能量将大于输入的能量,这明显是热力学第二定律所禁止的。这是因为能量和信息都需要属于该系统,不可能无中生有。http://ng1.17img.cn/bbsfiles/images/2012/07/201207030914_375472_2518341_3.jpg我们在生活中都可以观察到热力学定律的体现 如果要理解这是什么样的情况,那么我们可以设想下在充满热气体的容器中推动活塞。如果你不知道气体分子的运动方向,就可能会错误地推动活塞并做了无用功。但如果你知道气体分子的运动方向,就可以将活塞至于正确的方向上,这时候气体分子就会推动活塞运动,很明显这是热能转换为机械能,并做了有用功。以上两种方案中,系统的能量都是一样的,但结果却不一样。 此时,我们就可以将斯蒂芬妮·韦纳和易斯特·翰吉的信息理论与活塞模型相结合,如果我们对信息理论中的假想粒子进行解读,并希望获得更多的信息,就如同活塞模型中做更多的有用功,但是这些功却是额外赋予的,也就是说是“无中生有”的,因此如果“不确定性原理”在我们的宇宙中并不处在,那么热力学定律将被违反。http://ng1.17img.cn/bbsfiles/images/2012/07/201207030914_375473_2518341_3.jpg不存在“不确定性原理”的宇宙将是违反热力学定律 根据苏黎世联邦技术研究所理论物理学家马里奥·伯塔(Mario Berta)介绍:“我们现在随处都可以看到热力学第二定律在现实生活中的体现,基本上没有人会对此产生质疑,但我们现在也知道了,如果没有‘不确定性原理’,我们将打破热力学第二定律。”从本项研究的结论上看,似乎这样的解释比“不确定性原理”来得更为怪异,也说明了“不确定性原理”基本上是合理的,该研究就是为了理解为什么量子理论本身是如此怪异。http://ng1.17img.cn/bbsfiles/images/2012/07/201207030915_375474_2518341_3.jpg爱因斯坦认为上帝不掷骰子
各位老师好: 公司在编制CNAS内审表的时候留意了这个条款“7.6.3 [font=宋体][font=宋体]当由于检测方法的原因难以严格评定测量不确定度时,实验室应基于对理论原理的理解或使用该方法的实践经验进行评估。[/font][/font]”请问各位在工作中有遇到这种情况吗?哪位老师可以分享一个这种情况的评定资料学习一下吗?非常感谢~
资料名称化学分析检测机构在认可中应注意的几个问题《产品质量检验机构计量认证审查认可(验收)评审准则实验室认可准则在微生物检测实验室的应用说明实验室认可准则在化学检测实验室的应用说明移液管及容量瓶的不确定度测量不确定度原理及其在理化检验中的应用直线回归计算及其不确定度的评价用火焰[url=https://insevent.instrument.com.cn/t/Wp][color=#3333ff]原子吸收光谱[/color][/url]法对铅含量为1.00mg[kg时不确定度炽烧残渣测定结果不确定度评定标准溶液测量不确定度的评价滴定分析用标准溶液的标定及比较测量不确定度评定微生物分析测量不确定度评定测量不确定度初学者指南测量不确定度政策及其实施指南测量不确定度评定及应用测量不确定度基础知识地址:http://www.instrument.com.cn/show/search.asp?sel=admin_name&keywords=lfsming&DTID=&admin_type=&page=1
CNAS-CL01:2018 7.6.3 开展检测的实验室是否评定测量不确定度?[color=#ff0000]当由于检测方法的原因难以严格评定测量不确定度时,实验室是否基于对理论原理的理解或使用该方法的实践经验进行评估?[/color][color=#333333]大家有碰到类似的情形吗?有没有具体案例?[/color]
不确定度评定中仪器不确定度和重复性不确定度是否重复?是否只要仪器不确定度就可以!
【资料】测量不确定度原理及在理化检验中的应用(讲义,王承忠) (limu1983) http://www.instrument.com.cn/bbs/shtml/20080901/1457605/原创:测量不确定度的评定方法 (rosymuzi)http://www.instrument.com.cn/bbs/shtml/20051214/300444/【讨论】欢迎分享力学性能测量不确定度评定相关资料和进行相关讨论 (miceboy)http://www.instrument.com.cn/bbs/shtml/20080710/1349005/【原创】材料力学教学实验中的不确定度分析 (wysc)http://www.instrument.com.cn/bbs/shtml/20080701/1335048/
测量不确定度评定在不同应用中的差别讲授人:中国计量科学研究院研究员 倪育才 测量不确定度评定的应用范围很广。对于不同的场合和不同的要求,测量不确定度评定的原理和步骤是相同的,但在具体细节上会稍有差别。 1.特定测量结果的不确定度评定 评定一个已经得到的特定测量结果的不确定度,这是测量不确定度评定最基本的情况。由于测量已经完成,测量结果也已经得到,因此在这种情况下的测量对象、测量仪器、测量方法、测量条件、测量人员、测量和数据处理程序等都是已经确定而不能改变的。如果对同一测量对象,用同样的方法和设备,并由相同的人员重新进行测量,则不仅测量结果可能会稍有不同,其测量不确定度也可能会受测量条件改变的影响而变化。由于这时要求得到该特定测量结果的不确定度,因此不确定度评定应针对该特定测量条件进行。所得到的测量不确定度是该特定测量结果的不确定度,一般不要将其用于其他的同类测量中。 例如,对某一物体的长度进行测量,若测得被测物体和参考标准的温度t=19.50℃,其测量不确定度为u(t)=0.02℃,在进行不确定度评定时,作为主要影响量的温度的估计值应取实际测得的温度19.5℃,而其不确定度u(t)直接取0.02℃。如果对该长度重复进行测量,则由于温度t的数值可能会发生变化,因此从原则上说评定得到的不确定度也将不同。 2.常规测量的不确定度评定 在实际工作中,有许多测量是常规性的,例如量具和测量仪器的检定和校准,以及质检部门对一些大宗的材料或产品的检验,对于这类测量,测量仪器、测量方法和测量程序是固定不变的;测量对象是类似的,并且满足一定要求;测量人员可以不同,但均是经过培训的合格人员;测量条件是由检定规程、校准规范、国际标准、国家标准或部门标准等技术文件规定的,测量过程就是在该重复性条件下进行。一般说来,这时的测量不确定度会受测量条件改变的影响。但由于测量条件已被限制在一定的范围内,只要满足这一规定的条件,其测量不确定度就能满足使用要求。对于这类常规的测量工作,进行测量不确定度评定时应假设其环境条件正好满足所规定的合格条件。这样评定得到的测量不确定度是在规定条件下可能得到的最大不确定度。也就是说,在实际的测量中只要测量条件满足要求,测量不确定度肯定不会大于此值。通常就将此不确定度提供给用户,这样做的好处是不必对每一个测量结果单独评定其不确定度,除非用户对测量不确定度另有更高的要求。这时给出的测量不确定度并不是该实验室所能达到的最小不确定度,而是在常规测量中至少可以达到的测量不确定度。在建立计量标准时,JJF1033-2001《计量标准考核规范》规定,应在《计量标准技术报告》中给出这一不确定度。 在上例中,如果被测物体是量块,并且进行的是量块的常规检定,若技术文件规定该测量的温度条件是20℃±1℃,于是在进行测量不确定度评定时,作为主要影响量温度的测量不确定度应根据上述温度条件20℃±1℃,并由假定的概率分布(例如矩形分布)通过B类评定得到。 3.评定实验室的校准测量能力 校准测量能力(calibrationmeasurement capability)也称为最佳测量能力(best measurementcapability,常简称为BMC)。其定义为:“通常提供给用户的最高校准测量水平,它用包含因子k=2的扩展不确定度表示”。校准测量能力是实验室对于特定的测量任务可能达到的最小不确定度。也就是说,当使用实验室可能得到的最好测量设备,在可能达到的最佳测量条件下,它是对于性能最好的测量对象所得到的测量不确定度。或者说,它是当不确定度概算中所有的不确定度分量都达到可能的最小值时,实验室得到的测量不确定度。有时也用合成标准不确定度uc,min表示对于该测量任务的校准测量能力。因此,校准测量能力表示实验室可能达到的最高水平,但并不表示实验室在一般的常规校准中均能达到这一水平。在实验室认可工作中,要求申请认可的实验室申报该实验室的最佳测量能力,并应对实验室申报的最佳测量能力进行认可。 在上例中,如果要得到量块的最佳测量能力,则可假定其温度状态处于实验室内可能达到的最佳状态,例如20.0℃±0.2℃,并由此估算由温度引入的不确定度分量。 4.测量过程的设计和开发 在实际工作中,经常会遇到测量过程的设计和开发问题。此时主要的测量设备往往已经确定,而且事先知道希望达到的测量不确定度。通过不确定度管理程序,采用逐步逼近法对测量不确定度进行反复评定,可以得到不仅满足所要求的测量不确定度,并且也可得到在经济上比较合理的测量程序和至少应满足的测量条件。 也可以通过不确定度管理程序,确定所用的测量设备是否能满足要求。 现以环规校准为例,说明如何采用逐步逼近法来设计和开发合适的测量过程。 (1)测量任务和目标不确定度 测量任务为对Ф100mm×15mm环规的对称平面中确定方向的两点直径进行校准。目标不确定度为UT=1.5μm。 (2)测量原理、测量方法、测量程序和测量条件 采用机械接触式测量机,与一标称直径相同的参考环规进行比较。 假定卧式测量机的最大允许误差为±0.6μm。测量中被测环规和参考环规之间的温度差小于1℃。由重复性测量得到,两环规直径差测量的标准偏差为0.7μm。两环规线膨胀系数之相对差假定小于10%。 (3)逐步逼近法 逐步逼近法一般包括至少两次的各不确定度分量的重复评估。其中第一次评估是十分粗略、快速以及低成本的,其目的是识别最大的几个不确定度分量。要确保每一个不确定度分量的大小只允许高估,而不能低估。此后的每一次评估(如果有的话)则仅将最大几个分量的“上界”重新进行更精确的评定,即适当降低高估的程度,以将不确定度的估计值(uc或U)减小到能被接受的程度。 (4)首次评估 在考虑了5项主要的不确定度分量后,得到首次评估的测量不确定度分量汇总表(在评定过程中假定转换因子b等于包含因子k的倒数。对于U形分布、矩形分布和正态分布,取转换因子b分别近似地为0.7,0.6和0.5。)。 由于首次评估得到的扩展不确定度UE1不满足判据UE1
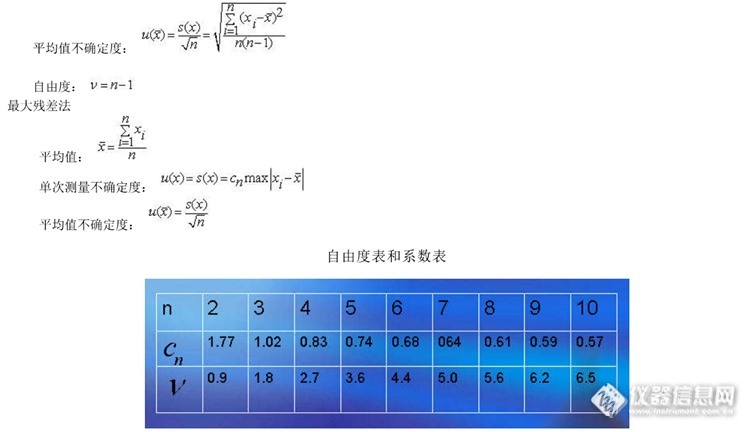
内容包括: 从数理统计角度对不确定度的原理进行阐明,通过误差传播定理和方差传播定理推导出不确定度的合成公式;两类不确定度的评定方法,合成自由度计算,以及不确定度评定结果的表达。http://ng1.17img.cn/bbsfiles/images/2017/10/2016090910280733_01_0_3.jpghttp://ng1.17img.cn/bbsfiles/images/2017/10/2016090910281228_01_0_3.jpghttp://ng1.17img.cn/bbsfiles/images/2017/10/2016090910281729_01_0_3.jpghttp://ng1.17img.cn/bbsfiles/images/2017/10/2016090910282192_01_0_3.jpghttp://ng1.17img.cn/bbsfiles/images/2017/10/2016090910282687_01_0_3.jpghttp://ng1.17img.cn/bbsfiles/images/2017/10/2016090910283189_01_0_3.jpghttp://ng1.17img.cn/bbsfiles/images/2017/10/2016090910283882_01_0_3.jpghttp://ng1.17img.cn/bbsfiles/images/2017/10/2016090910284537_01_0_3.jpghttp://ng1.17img.cn/bbsfiles/images/2017/10/2016090910285125_01_1898299_3.jpghttp://ng1.17img.cn/bbsfiles/images/2016/09/201609091029_608978_2984502_3.jpghttp://ng1.17img.cn/bbsfiles/images/2016/09/201609091029_608979_2984502_3.jpghttp://ng1.17img.cn/bbsfiles/images/2016/09/201609091029_608980_2984502_3.jpghttp://ng1.17img.cn/bbsfiles/images/2016/09/201609091029_608981_2984502_3.jpghttp://ng1.17img.cn/bbsfiles/images/2016/09/201609091029_608982_2984502_3.jpghttp://ng1.17img.cn/bbsfiles/images/2016/09/201609091029_608983_2984502_3.jpghttp://ng1.17img.cn/bbsfiles/images/2016/09/201609091029_608984_2984502_3.jpg
不确定度论一出世,为占据测量计量领域,首先否定真值,随即对误差概念进行诬陷。说:误差等于测得值减真值,真值不可知,误差不可求。近二十年来,随着真值被贬,误差概念蒙冤多时了。这是一次历史性的误解,一场世界性的冤案,该给误差概念平反了。以下讲误差概念的真面目,以驳斥不确定度论对误差概念的诬陷。1 误差概念的三个层次A 误差的物理意义。 误差是测得值与被测量真值(准确值)之差。这对理解什么是误差很重要,但由于被测量的准确值在通常情况下是不知道的,故不能直接按定义确定误差,而要通过标准,间接而又符合定义地确定误差。误差一语有双重含义,通常误差分析指误差元,测量仪器误差指误差范围。误差范围由误差元构成B 误差实验值的测定。方法之一是用高一等级的标准测量仪器测同一被测量,得到相对准确值,测得值与相对准确值之差为误差实验值。方法之二,依据等量代换原理,用被检仪器测量 上一级 标准器,测得值与标准器标称值之差是误差实验值。C 误差计算。按误差方程,从误差实验值计算误差。(见本网史锦顺“误差方程的新概念”一文。)三百年来,是按A、B来理解并计算误差的,是基本正确的,但比较粗(略小写)。有了误差方程,计算就精确了。
[font=宋体][color=#3f3f3f][back=rgba(255, 255, 255, 0.7)]从影响测量结果的因素考虑, 测量结果的不确定度一般来源于:被测对象、 测量设备、测量环境、测量人员和测量方法。[/back][/color][/font][font=宋体]被测对象[/font][b][font=宋体][size=16px]1.被测量的定义不完善[/size][/font][/b][font=宋体][size=16px]被测量即受到测量的特定量,深刻全面理解被测量定义是正确测量的前提。如果定义本身不明确或不完善,则按照这样的定义所得出的测量值必然和真实之间存在一定偏差。农业农村[/size][/font][b][font=宋体][size=16px]2.实现被测量定义的方法不完善[/size][/font][/b][font=宋体][size=16px]被测量本身明确定义,但由于技术的困难或其它原因,在实际测量中,对被测量定义的实现存在一定误差或采用与定义近似的方法去测量。[/size][/font][font=宋体][size=16px]例如:器具的输入功率是器具在额定电压,正常负载和正常工作温度下工作时的功率。但在实际测量中,电压是由稳压源提供的,由于稳压源自身的精度影响,使得器具的工作电压不可能精确为额定值,故测量结果中应考虑此项不确定因素。故只有对被测量的定义和特点,仔细研究、深刻理解,才能尽可能减小采用近似测量方法所带来的误差或将其控制在一个确定范围内。[/size][/font][b][font=宋体][size=16px]3.测量样本不能完全代表定义的被测量[/size][/font][/b][font=宋体][size=16px]被测量对象的某些特征如:表面光洁度,形状、温度膨胀系数、导电性、磁性、老化、表面粗糙度、重量等在测量中有特定要求,但所抽取样本未能完全满足这些要求,自身具有缺陷,则测量结果具有一定的不确定度。[/size][/font][b][font=宋体][size=16px]4.被测量不稳定误差[/size][/font][/b][font=宋体][size=16px]被测量的某些相关特征受环境或时间因素影响,在整个测量过程中保持动态变化,导致结果的不确定度。[/size][/font][font=宋体]测量设备[/font][font=宋体][size=16px]计量标准器、测量仪器和附件以及它们所处的状态引入的误差。计量标准器和测量仪器校准不确定度,或测量仪器的最大允差或测量器具的准确度等级均是测量不确定度评定必须考虑的因素。[/size][/font][font=宋体]测量环境[/font][b][font=宋体][size=16px]1.在一定变化范围或不完善的环境条件下测量[/size][/font][/b][font=宋体][size=16px]温度 [/size][/font][font=宋体][size=16px]振动噪声 [/size][/font][font=宋体][size=16px]供给电源的变化[/size][/font][font=宋体][size=16px]温度 [/size][/font][font=宋体][size=16px]空气组成、污染 [/size][/font][font=宋体][size=16px]热辐射[/size][/font][font=宋体][size=16px]大气压 [/size][/font][font=宋体][size=16px]空气流动[/size][/font][b][font=宋体][size=16px]2.对影响测量结果的环境条件认识不足[/size][/font][/b][font=宋体][size=16px]由于对相关环境条件认识不足, 致使测量中或分析中忽视了对某些环境条件的设定和调整,造成不确定度。[/size][/font][font=宋体]测量人员[/font][font=宋体][size=16px]1.模拟式仪器的人员读数误差即估读误差,读取带指针仪表或带标线仪器的示值,即读取非整数刻度值时,由于估读不准而引起的误差。[/size][/font][b][font=宋体][size=16px]2.人员瞄准误差[/size][/font][/b][font=宋体][size=16px]采用显微镜或等光学仪器通过使视场中的两个几何图形重合来对线进行测量, 对线准确度与操作者经验和对线形状有关。[/size][/font][b][font=宋体][size=16px]3.人员操作误差[/size][/font][/b][font=宋体][size=16px]如测量时间的控制、测点的布置。该项取决于人员的经验、能力、知识及工作态度、身体素质等。[/size][/font][font=宋体]测量方法[/font][b][font=宋体][size=16px]1.测量原理误差[/size][/font][/b][font=宋体][size=16px]测量方法本身就存在一定的原理误差,对被测量定义实现不完善。[/size][/font][font=宋体][size=16px]例如在产品的电气强度试验中,由于耐压试验台自身内阻影响,使得加于样品两端的电压低于实际设定值。这样必然造成试验结果存在一定的不确定度。[/size][/font][b][font=宋体][size=16px]2.测量过程[/size][/font][/b][font=宋体][size=16px] 测量顺序[/size][/font][font=宋体][size=16px]应严格按照测量规范规定的进行。遗漏或颠倒某一操作过程都有可能造成测量结果的误差,甚至使测量失去意义。[/size][/font][font=宋体][size=16px] 测量次数[/size][/font][font=宋体][size=16px]一般来说测量次数不同,测量精度也不同,增加测量次数,可以提高测量精度。但 n>10 以后,σ已减少得非常缓慢。此外,由于测量次数愈大,也愈难保证测量条件的恒定,从而带来新的误差,因此一般情况下取 n=10 以内较为适应。[/size][/font][font=宋体][size=16px] 测量所需时间[/size][/font][font=宋体][size=16px]有的测量规定必须在一定条件下,一定时间内完成超出则结果不准确。如器具潮态试验后的泄漏电流测试必须在 5s 内完成。[/size][/font][font=宋体][size=16px] 测量点数[/size][/font][font=宋体][size=16px]操作规范规定测量若干点,但实际检测中,为节省时间或出于其它考虑减少或增加了测量点数,也对最终结果有影响。如在噪声测试中。[/size][/font][font=宋体][size=16px] 瞄准方式[/size][/font][font=宋体][size=16px]测量方法不同,采用的测量仪器不同,对应的瞄准方式也不同,如采取目测或用光学瞄准,其瞄准精度必然不同。[/size][/font][font=宋体][size=16px] 方向性[/size][/font][font=宋体][size=16px]测量结果须在一定稳态下获得,实验中以不同方向趋于稳态,对于有些测量设备,如具有滞后或磁滞性的仪器读数是不同的。[/size][/font][b][font=宋体][size=16px]3.数据处理[/size][/font][/b][font=宋体][size=16px] 测量标准和标准物质的赋值不准[/size][/font][font=宋体][size=16px]标准器具本身不可避免存在着制造偏差,它是由更高一级的标准来检定的,这些高一级的标准本身也存在着误差。[/size][/font][font=宋体][size=16px] 物理常数或从外部资料得到的数据不准[/size][/font][font=宋体][size=16px]外部资料中提供的数据很多,是由以前的测量为基础或单纯凭经验得出的,不可避免地存在着误差。[/size][/font][font=宋体][size=16px] 算法及算法实现[/size][/font][font=宋体][size=16px]采用不同的算法处理数据,如计算标准差 σ ,分别运用贝塞尔法和极差法,所得结果必然不同。[/size][/font][font=宋体][size=16px] 有效位数[/size][/font][font=宋体][size=16px]数据有效位数不同,精度不同,应根据测量要求或所采用的测量设备而定。[/size][/font][font=宋体][size=16px] 舍入[/size][/font][font=宋体][size=16px]由于数字运算位数有限,数值舍入或截尾造成不确定度。[/size][/font][font=宋体][size=16px] 修正[/size][/font][font=宋体][size=16px]有些系统误差是可以修正的,但由于对误差因素本身的认识不充分,修正值也必然存在着不确定度。[/size][/font][font=宋体]总结[/font][font=宋体][size=16px]须正确评定测量结果的不确定度,既不能过大,也不能过小,以保证产品质量,又不会造成误判。首先应充分考虑测量设备、测量人员、测量环境、测量方法等方面众多来源带来的不确定度分量,作到不遗漏、不重复、不增加。并正确评定其数值,其中设备来源不确定度可经过量值溯源,由上一级计量基标准的不确定度取得;也可利用所得到的检定校准证书,测试证书或有关规范所给的数据;方法不确定度经过研究和评定,其不确定度影响可能很小。评定不确定度的原则和框架,不能代替人的思维、理智和专业技巧。它取决于对测量和被测量的本质的深入了解和认识。因此,测量结果的不确定度评定的质量和实用性,主要取决于对不确定度影响量的认识程度和细致而中肯的分析。[/size][/font]
22.1蛋白质测定的原理测定样品中粗蛋白质含量,首先应该按照标准方法的规定,称取一定量样品按照规定的消化方法进行消化,使样品中的有机态氮在浓硫酸加热作用下转化为无机态的铵盐消化溶液。通过将消化溶液置于蒸馏装置中加碱蒸馏后使氨全部逸出,逸出的游离氨被硼酸澄澈直接吸收后以盐酸标准滴定溶液滴定至终点并定量计算。根据滴定手段的不同又不可分成两种方式:带有自动滴定装置的蛋白质测定仪对接收溶液自动滴定;人工对接收溶液进行滴定。22.2蛋白质测定中的测量不确定度对粗蛋白质测定过程进行测量不确定度的评估,首先必须对盐酸标准滴定溶液标定过程进行评估,计算并得出标定过程中的相对标准不确定度。其次,根据滴定方式的不同对样品测定过程中的测量不确定度进行评估,最终将上述两个过程的不确定度分量进行合成。22.3盐酸标准滴定溶液标定过程中测量不确定度的评估a.计算公式和数学模型假如标定0.5mo1/L盐酸标准滴定澄澈,根据计算公式,盐酸标准滴定溶液浓度c(HCl)为:式中:0.0530系1.00mL盐酸标准滴定溶液(浓度1mo1/L)相当型为: b.数学模型中各分量相对标准不确定度的评估1Na2CO3的摩尔质量M(Na2CO3)的不确定度uIUPAC于1997年发布的元素相对原子质量见表22——1。表22——1元素相对原子质量扩展不确定度标准不确定度Na22.989 7700.000 0020.000 001C12.0110.0010.000 5O15.999 40.000 .3[font=Times New Ro
[b][size=18px]讲讲不确定度。[/size][/b][size=18px][b]产生测量不确定度的原因[/b][/size] 测量过程中有许多可能引起不确定度的来源,可归纳以下几个方面: (1)被测量的定义不完善。 例如,定义被测量是一根标称值为lm的钢棒长度,要求测准微米数量级,则被测量的定义不够完善。因为被测钢棒受温度和压力的影响很明显,而这些条件没有在定义中说明。由于定义的不完整使测量结果引人压力和温度影响的不确定度。完整的被测量定义是:标称值为lm的钢棒在25.0℃和101325Pa时的长度。若在定义要求的温度和压力下测量,就可避免由此引起的不确定度。 (2)实现被测量的测量方法不理想。 例如,在微波测量中,衰减量是在匹配条件下定义的,但实际测量系统不可能理想匹配,因此失配引起不确定度。 (3)被测量的样本可能不完全代表定义的被测量。 例如,被测量为某种介质材料的介电常数由于受测量方法和测量设备的限制,只能取这种介质材料的一部分做成样块进行测量。受样块材料成分的均匀性所限而引起不确定度。 (4)对环境条件的影响认识不足或对环境条件不完善的测量。 同样以钢棒为例,不仅温度和压力影响其长度,实际上,湿度和钢棒的支撑方式都有明显影响,但由于认识不足,没有采取措施,就会引起不确定度。测量温度和压力所用的温度计和压力表也是一个不确定度的来源。 (5)测量人员对模拟式仪器的读数偏差。 由于读数的位置不同,产生读数偏差,引起的不确定度。 (6)测量仪器的分辨力和识别17限不够。 (7)测量标准引起的不确定度。 测量标准如标准装置、标准器具或标准物质,它们的测量通常是将被测量与测量标准的给定值进行比较而实现的,因此测量标准的不确定度直接引人测量结果中。 (8)在数据处理时所引用的常数及其他参数的不确定度。 (9)测量方法和测量程序引起的不确定度。 (10)被测量的各种随机影响使测量时重复观测值随机变化。 由此可以看出,测量不确定度一般来源于随机性或模糊性。前者归因于条件不充分,后者归因于事物本身概念不明确。因而测量不确定度一般由许多分量组成。其中一些分量具有统计性,另一些分量具有非统计性。所有这些不确定度来源?若影响到测量结果,都会对测量结果的分散性作出贡献。 总之,在寻找不确定度的来源时,可从测量仪器、测量环境、测量人员、测量方法及被测量等方面全面考虑,应做到不遗漏、不重复,特别应考虑对测量结果影响大的不确定度来源。遗漏会使不确定度变小,重复会使不确定度过大。一份测量不确定度表示与评定报告准确与否,与寻找各个分量不确定度有直接关系。[b][size=18px]测量不确定度的分类[/size][/b] 不确定度依据其评定方法可以分A类、B类两种,它们与过去随机误差与系统误差的分类之间不存在简单的对应关系,随机误差与系统误差表示两种不同性质的误差,而A类、B类表示两种不同的评定方法。因此,简单地把A类不确定度对应于随机误差导致的不确定度,把B类不确定度对应于系统误差导致的不确定度的做法是错误的。 实际上一台仪器出厂指标往往既包括了随机影响又包含了系统影响,难以将其区分为随机不确定度与系统不确定度。一个量在不同的情况下,随机不确定度可能变成系统不确定度。例如,制造厂生产的一批量具的值带有随机性而给出随机效应导致的不确定度,该产品对用户而言,其值就是固定值,不带随机性。 目前,国际上一致认为,为避免误解与混淆已不再使用“随机不确定度”与“系统不确定度”这两个术语。如需要区分不确定度的性质,可用“由随机效应导致的不确定度分量”与“由系统效应导致的不确定度分量”这两种表述方法。它们并不表明不确定度是用什么方法评定的,也就是说由系统效应引起的不确定度既可用B类、也可以用A类评定方法得到。性质和评定方法间没有对应关系。 分类的目的是仅为讨论方便,并不意味着两类评定之间存在本质上的区别,它们都基于概率分布,并都用方差或标准差表征。——本文转载自《计量所长工作实务全书》

红外光度法测定水中石油类的不确定度分析摘要:本文通过对红外光度法测定水中石油类的测定原理、方法的的讨论,建立数学模式,找出测量不确定度的来源,从而计算其测量不确定度。关键词:石油类,相对不确定度,合成不确定度1. 目的对红外光度法测定石油类的不确定度进行分析,找出影响不确定度的因素,对不确定度进行评估,如实反应测量的置信度和准确性。2. 适用范围本文件适用于依据GB/T16488-1996对水质石油类和动植物油进行测定的不确定度分析。3. 石油类测定原理用四氯化碳萃取水中的油类物质,测定总萃取物,然后将萃取液用硅酸镁吸附,去除动植物油等极性物质后,测定石油类。总萃取物和石油类的含量均由波数分别为2930cm-1(CH2基团中C—H键的伸缩振动)、 2960cm-1(CH3基团中C—H键的伸缩振动)和3030cm-1(芳香环中C—H键的伸缩振动)谱带处的吸光度A2930、A2960和A3030进行计算。4. 测量方法简述(见流程图)取500ml水样,用四氯化碳萃取后定容到25ml后测量。http://ng1.17img.cn/bbsfiles/images/2012/10/201210111452_396009_2157399_3.jpg5. 石油类测定的数学模型http://ng1.17img.cn/bbsfiles/images/2012/10/201210111502_396014_2157399_3.jpg (1)式中:C1——滤出液石油类的浓度V1——萃取溶剂(四氯化碳)定容体积V0——水样体积6. 石油类测量不确定度计算公式。按不确定度传播定律,从(1)式导出:http://ng1.17img.cn/bbsfiles/images/2012/10/201210111502_396015_2157399_3.jpg (2)
我们实验室是新建的,人数也很少,就几个员工和一个技术负责人,现在的话技术负责人要求我们写不确定度评定的模板,虽然上过一次CMA建设咨询公司的不确定度培训,但是我自己还是挺懵的,就想问一下:不确定度评定分量要算的是不是相对标准不确定度,在最后一步再把所有分量的相对标准不确定度计算为相对合成标准不确定度,最后才是扩展不确定度。以酚试剂为例,制作标准曲线的试剂的不确定度要不要把吸收液、甲醛标准溶液的加进去?标准曲线的不确定度要怎么算?用贝塞尔公式算吗?样品的不确定度要不要把吸收液的也弄进去?
标准不确定度和相对标准不确定度有什么区别呢?例如我用天平称量空烧杯10.23g,又称了烧杯加残渣重10.45g,结果为10.45-10.23=0.22g,B类不确定度为U,那么天平的B类相对不确定度应该怎么算呢?[em0715]
[align=center]测量结果的不确定度or误差的不确定度?[/align][align=center]武汉大学 叶晓明[/align] 不确定度概念作为法定计量术语已经20多年,其定义是测量结果的“分散性”内涵。这一概念内涵被许多人津津乐道,但实际上几乎从来没有人真正讲清楚这个“分散性”,也几乎没有人真正理解它。因为它本身实际是个错误的概念定义,就如同皇帝的新衣,在千万人簇拥下,谁敢相信皇帝实际什么也没有穿?现在,老叶就当回质疑皇帝新衣的那个男孩。 一个测量完成后,给出一个具有确定数值的测量结果,一个确定的数值凭什么还有不确定性?什么叫确定?什么叫不确定?什么叫确定的不确定?不确定度是用标准偏差(方差)或多倍标准偏差来表达的,那么,我们现在就从标准偏差(方差)的数学概念说起。把方差的概念说明白了,不确定度概念的真实内涵自然也就清楚了。 首先明确随机变量这个概念。所谓随机变量就是未知量或者数值不确定的量。请注意,随机变量不是指随机不停地变化的量!正因为随机变量的数值未知,我们只有针对其所有可能取值进行研究,因而才有了用数学期望和方差二个数字指标来描述随机变量所存在的概率范围。 对于一个随机变量L而言,其所有可能取值为序列{L[sub]i[/sub]},于是,其数学期望定义为EL=∑L[sub]i[/sub] /n,其方差定义为σ[sup]2[/sup](L)=E(L-EL)[sup]2[/sup]。数学期望是其所有可能取值的均值,方差是其所有可能取值的分散性。这样,数学期望和方差就共同描述了随机变量L所存在的概率范围。 一个重要的特殊情形:对于一个确定的常量C而言,其所有可能取值都是C。于是,其数学期望就是EC=C,其方差就是σ[sup]2[/sup](C)=E(C-EC)[sup]2[/sup]=0。这当然是一个最基本的数学常识了。 但是,方差概念被用于测量理论后,我们早期的测量理论界却把数学经给念歪了。譬如:珠峰高程的测量结果x=8844.43m,其标准偏差σ(x)=±0.21m。这不就成了σ(8844.43)=±0.21了吗?8844.43难道不是确定的常量C吗?为什么会出现σ(8844.43)≠0了?相信有的朋友已经看明白了,此x非彼x也!x=8844.43m中的此x仅仅是指8844.43,不代表任何其它可能取值,但σ(x)中的那个彼x却不是仅指8844.43。----偷换概念了,把别的随机变量的方差偷换成了测量结果8844.43的方差! 方差的概念原来是移花接木到测量结果头上的,不确定度概念自然也被移花接木了。 一个更乱伦的问题是,随机变量需要方差和数学期望二个参数来描述,给测量结果偷了一个方差却没有给它偷一个数学期望,一个没有数学期望的孤立的方差有什么用呢?这种仅有所谓发散性却没有数学期望的不确定度能表示出什么含义来呢? 进一步的问题:这个σ(x)中的x实际是什么东西?它是从哪里偷来的?那个被盗的主人又是谁?[align=center][img]http://image.sciencenet.cn/home/201806/27/105552dsdd7a5shr5h2as2.jpg[/img][/align] 请看图1。首先,测量结果[i]x[/i]给出后,测量结果[i]x[/i]是确定量。虽然测量结果[i]x[/i]的确是其所有可能取值{[i]x[sub]i[/sub][/i]}中的一个成员,但以其所有可能取值{[i]x[sub]i[/sub][/i]}的方差和数学期望来表达[i]x[/i]是没有意义的,因为确定量[i]x[/i]丧失了使用{[i]x[sub]i[/sub][/i]}的方差和数学期望来表达的资格和需要。就如同明确知道一个婴儿已经顺利降生却还要去估计这个婴儿发生难产的概率一样,是没有意义的。概率针对的是不确定的未知事件,只是以确定的已知事件作为统计样本而已。 但是,图1中的误差∆ [sub]A[/sub]、∆ [sub]B[/sub]和∆ 都是不确定量,是随机变量。研究这些未知误差的概率分布才是有意义的事情。 因为测量结果[i]x[/i]是其所有可能取值{[i]x[sub]i[/sub][/i]}中的任意一员,误差(偏差)∆ [sub]A[/sub]=[i]x[/i]-[i]Ex[/i]也就是{[i]x[sub]i[/sub][/i]-[i]Ex[/i]}中的任意一员。就是说,序列{[i]x[sub]i[/sub][/i]-[i]Ex[/i]}是误差∆ [sub]A[/sub]=[i]x[/i]-[i]Ex[/i]的所有可能取值的集合。这样,针对随机变量∆ [sub]A[/sub]=[i]x[/i]-[i]Ex[/i],就有: 其数学期望:E∆ [sub]A[/sub]=E(x-Ex) =Ex-Ex=0 其方差: σ[sup]2[/sup](∆ [sub]A[/sub] )=E(∆ [sub]A[/sub]-E∆ [sub]A[/sub] )[sup]2[/sup] =E(∆ [sub]A[/sub] )[sup]2[/sup] =E(x-Ex)[sup]2[/sup] 就是说,误差(偏差)∆ [sub]A[/sub]=x-Ex存在于一个数学期望为0方差为σ[sup]2[/sup](∆ [sub]A[/sub])的概率区间内,或者说,方差σ[sup]2[/sup](∆ [sub]A[/sub])是误差∆ [sub]A[/sub]的概率区间的评价值。 同理,误差(偏差)∆ [sub]B[/sub]=Ex-x[sub]T[/sub]也是测量产生的,是上游测量的随机变量,也有E∆ [sub]B[/sub]=0,且也有其概率范围评价σ[sup]2[/sup](∆ [sub]B[/sub])。于是:[align=center] ∆ =∆ [sub]A[/sub]+∆ [sub]B[/sub][/align][align=center] E∆ =E∆ [sub]A[/sub]+E∆ [sub]B[/sub]=0[/align][align=center]σ[sup]2[/sup](∆ )=E(∆ )[sup]2[/sup][/align][align=center] =E(∆ [sub]A[/sub]+∆ [sub]B[/sub])[sup]2[/sup][/align][align=center] =σ[sup]2[/sup](∆ [sub]A[/sub] )+σ[sup]2[/sup](∆ [sub]B[/sub] )[/align] 可见,方差(标准偏差)是误差的概率区间的数字评价而已,表达误差的取值不能被确定的程度。人们做不确定度分析时不都是这样通过误差方程获得方差传播关系来合成方差吗?却原来,现有测量理论实际上是把误差的方差(标准偏差)强行筐到了测量结果的脑袋上。[color=#333333]所以,前边珠峰案例的严格表达应该是:[/color][color=#333333]测量结果[/color][i]x[/i][color=#333333]=8844.43m[/color][color=#333333],标准偏差[/color][i]σ[/i][color=#333333](∆ [i]x[/i])=±0.21m[/color][color=#333333]。[/color] 朋友们若不信,可以去翻翻现有的测量学教科书,无论仪器学还是测绘学的,看看哪些教科书是用σ[sup]2[/sup](x)或σ[sub]x[/sub][sup]2[/sup]的形式表示方差,看看有没有教科书用σ[sup]2[/sup](∆ x)或σ[sub]∆ x[/sub][sup]2[/sup]的形式表示方差。 不确定度实际是误差的概率区间评价,这个评价有何意义? 因为误差是测量结果与真值之差,即∆ =x-x[sub]T[/sub],所以[align=center]x[sub]T[/sub]=x-∆ [/align] 这样,真值x[sub]T[/sub]的数学期望: Ex[sub]T[/sub]=Ex-E∆ =x 真值x[sub]T[/sub]的方差: σ[sup]2[/sup](x[sub]T[/sub] )=E(x-∆ )[sup]2[/sup] =E(x)[sup]2[/sup]+E(∆ )[sup]2[/sup] =σ[sup]2[/sup](∆ ) 这就是说,真值x[sub]T[/sub]存在于一个以测量结果x为数学期望以σ[sup]2[/sup](∆ )为方差的概率区间内,不确定度实际反映了测量结果与真值的可能接近程度!也就是说,我们只能说“误差的不确定度”或“真值的不确定度”,而不能说“测量结果的不确定度”!测量结果作为一个具有确定数值的常数,本身就不存在不确定度这个问题。 呵呵,测量理论界干了一件丢人的事情:把误差的不确定度偷换成了测量结果的不确定度,把基层测量工作者甚至整个科学界都给坑了。错了就赶紧改正呗,继续将错就错、误人子弟就不应该了。 2018 6 26 于武汉大学
新的方法我们要做方法确认和不确定度评定关于不确定度有5个问题:1.这个不确定度(例如相对不确定度为6%)能直接用作以后的测试的数据的不确定度吗?2.要是不能直接用作以后测试数据的不确定度这个评定的意义在哪里?3.有些时候测试结果要给出不确定度,但只测试了一次的,你们怎么处理?4.关于数值修约的不确定度你们是怎么转换为相对不确定度(数值只保留到个位)?是0.5除以根号3再除以测试的样品含量吗?5.你们的不确定度评定是多久做一次?
测量不确定度是针对测量系统的不确定度。那个同一个测量系统再测试不一样的样件,测试结果不一样。不确定度是不变的吧。CNAS要求检测实验室出具的不确定度报告,每个样件的测试结果都在符合范围内。此套测试系统的测量不确定度是一致的吧。做符合性判定时,现行的标准规范没有指出限值有没有包含不确定度。请问下,有没有标准规范直接说明了,限值已经考虑到了不确定度的影响?做符合性判定时,如果客户要求判定规则考虑不确定度。那标准规范中的限值,已经不是判定的限值了。对不确定度了解不深,还请大家给点建议。谢谢
测量不确定度初学者指南测量及测量不确定度(一) 1. 测量1. 1什么是测量? 测量告知我们关于某物的属性。它可以告诉我们某物体有多重,或者有多热,或者有多长。测量就赋予这种属性一个数。测量总是用某种仪器来实现的。尺子、秒表、称重称,以及温度计都是测量仪器。测量结果通常有两部分组成:一个数和一个测量单位,例如"这有多长?……2米"。1. 2什么不是测量?有些过程看起来像是测量,然而并不是。例如,两根绳子做比较,看那一根长些,这实际上就不是测量。计数通常也不认为是测量。检测(test)往往不是测量;检测通常要得出"是或非"的答案,或者"合格或不合格"的结果。(但是,测量可以是检测的局部过程,逐而得出检测结果)。2. 测量不确定度2.1 什么是测量不确定度?测量不确定度是对任何测量的结果存有怀疑。你也许认为制作良好的尺子、钟表和温度计应该是可靠的,并应给出正确答案。但对每一次测量,即使是最仔细的,总是会有怀疑的余量。在日常说话中,这可以表述为"出入",例如一根绳子可能2米长,由1cm的"出入"。2.2 测量不确定度的表述由于对任何测量总是存在怀疑的余量,所以我们需要回答"余量有多大?"和"怀疑有多差?"这样,为了给不确定度定量实际上需要有两个数。一个是该余量(或称区间)的宽度;另一个是置信概率,说明我们对"真值"在该余量范围内有多大把握。例如:我们可以说某棍子的长度测定为20厘米加或减1厘米,由95%的置信概率。这结果可以写成:20cm±1cm,置信概率为95%。这个表述是说我们对棍子长度在19厘米到12厘米时间由95%的把握。还有其他一些表述置信概率的方式,对此将在下文第7节中再说。2.3误差与不确定度的比较不要混淆术语"误差"和"不确定度"是很重要的。误差:是某待测物的测得值与"真值"之间的差。不确定度:是定量表示对测量结果的怀疑程度。无论何时我们都可能试图去修正任何已知的误差,例如:通过从校准证书得到的修正值。 但是我们并不知道其值的任何误差都是不确定度的来源。2.4 为什么测量不确定度是重要的你也许对测量不确定度有兴趣仅仅是因为你希望要做质量好的测量,并要了解结果。但是,还有其他一些更特殊的理由要考虑测量不确定度。你也需要做测量作为下列工作的一部分: ●校准--必须在证书上报告测量不确定度。 ●检测--需要测量不确定度来确定合格与否。 ●允差--在你能确定是否符合允差以前,你需要知道不确定度。 ……或者你可能需要阅读或了解校准证书或者检测或测量的书面技术规范。