如题,想请教各位老师单点校准曲线的剩余标准差的自由度?例如标准品一个浓度点独立进样3次,建立单点校准曲线,求该标准曲线的残差Sy时,自由度是多少?3+1(0点)-2=2吗,或者就是3吗?还有斜率的标准偏差是怎么算,是等于Sy/工作液的浓度吗?还是全都按照多点校准曲线中计算Sy和Sb的公式算,感觉按照多点校准曲线的公式算有点问题
小弟求助各位大哥,我2月24日就要考试计量认证了,但是还没搞懂复习资料上的,希望大家帮帮我。3个计算:合成标准不确定度,有效自由度,扩展不确定度的公式及原理与计算e-mail:yangjun19821112@sina.comQQ82633178十万火急!!!!!
自由度f是偏差平方和中独立平方的数据的个数.存在目标值X0时,自由度就是数据的个数,即f=n 对平均值为a时的自由度f是数据的个数减去1,即f=n-1.原因是,有将n个偏差(X1-a),(X2-a),........(Xn-a)相加之和等于零的一个关系式存在,即:(X1-a)+(X2-a)+........+(Xn-a)=0故自由度:f=n-1为什么就得出f=n-1呢?
大家新年好! B类不确定度的自由度如何算?我看了下测量不确定度评定与表示 JJF1059-1999,感觉很难算B类不确定度的自由度。 在网上查了些资料有的人说:对B类不确定度的自由度,可靠的按无穷大算(例如从说明书,技术规范上得到的不确定度(允许误差,容量误差等。。。),相对可靠可以认为是50,比如从检定或校准证书得到;完全凭经验估计的不确定度,如震动、不水平等可能引起的不确定度自由度非常低,一般不大于10,可取5、2、1;
在统计学中,自由度指的是计算某一统计量时,取值不受限制的变量个数。通常v=n-k。其中n为样本含量,k为被限制的条件数或变量个数。在测量不确定度的评定中,自由度衡量了不确定度的可靠程度,所以可以说自由度是一种二次或二阶不确定度。自由度越大,不确定度的可靠程度越高。A类不确定度的评定,采用的是重复测量,计算标准偏差的方法进行评定的,可以直接通过公式v=n-k,计算自由度。根据标准偏差的计算通常会分为以下情况:(1) 用贝塞尔公式 计算实验标准偏差时,若测量次数为n,则自由度v=n-1。 (2) 当同时测量k个被测量时,则自由度v=n-k。 (3) 对于合并样本标准差sp,即进行多组测量时,其自由度为各组的自由度之和。 (4) 当用极差法估计实验标准差时,由于没有有效的利用所提供的全部信息量,其准确度相对使用贝塞尔公式时较差,自由度比贝塞尔公式法小。具体数值见表:n23456789101520v0.91.82.73.64.55.36.06.87.510.513.1B类不确定度评定在确定自由度时,由于缺少足够的数据支持,所以B类评定不确定度的自由度是靠估计B类评定不确定度的相对标准不确定度得到的。所以在确定B类评定不确定度时就需要采取一些技巧。下面具体说明:(1)当不确定度的评定有严格的数字关系,如数据修约时引起的不确定度,可靠程度最高,自由度为∞。(2)当计算不确定度的数据来源于校准证
摘录第18页除非特别要求或为获得Up而必须求得uc的有效自由度外,一般情况下B类的标准不确定度评估可以不给出自由度。请问这话的出处或是意义在哪儿?请朋友不吝告知,谢谢!
科普展品是展示科学、普及科学知识的产品,大型交互式模拟展览可以使用多自由度并行平台作为载体,达到最佳的展示效果。本文将结合笔者在科技馆工作的实际经验,讨论多自由度并行平台在科普战项目中的应用。 一多自由度并联平台 多自由度并联平台由多个伸缩杆和两个平台组成,下部平台必须固定,伸缩杆壳体套必须固定在下部平台上,上部使用万向比较链连接到上部平台嵌入式-PLD(可编程逻辑器件) 多自由度并联平台没有明确的命名规范,通常根据自由度数执行器的类型命名。例如,如果图1平台有6个自由度,执行器是伺服传动缸,则命名为“6个自由度伺服传动缸平台”。嵌入式-FPGA(现场可编程门阵列) 2六自由度并联平台位置姿态及求解 六自由度并联平台的六个伸缩杆可以在控制下自由伸缩,因此必须调整六个伸缩杆,使六自由度平台能够根据需要移动。射频 六自由度并联平台的平台位置姿态与各伸缩杆的伸缩量呈非线性关系,正解计算过程复杂,但六自由度并联平台位置反转相对简单。一般提供平台的6个空间姿态参数(、Y、Z、A、8、Y),通过计算得出6个伸缩杆长度(L1 ~) 如图2所示,将A1~A6设置为上部平台和伸缩杆的比较触点,将B1~B6设置为下部平台和伸缩杆的比较触点。 上下平台的转换公式如下: 其中[T]是旋转矩阵,首先:绕轴旋转y,平移关系如下: 用矩阵书写的格式如下: 同样,如果旋转8、A得到矩阵[b]、[/b][A],则旋转矩阵[T]=[C][A]。如果用转换公式替换生成的矩阵[T],则可以获得伸缩条的长度,表示如下: 根据上述计算,利用计算机实时获取L10L6伸缩条的长度,并可向伸缩条控制器提供计算机输出信号,以准确控制六自由度并联平台的姿态。 三六自由度伺服液压系统平台在科普展品中的应用 如图~所示,宁夏科技馆的全景飞行模拟器展品利用六自由度伺服液压平台,根据观众的工作情况实时模拟飞机的姿态(左右倾斜、上下旋转等),模拟实际飞行环境。将投影仪内投影与多种声光电技术相结合,从视觉和位置感上给予参与者强大的冲击,创造出几个杂乱的模拟环境。 六自由度伺服液压平台正常运行已超过11年,仅发生液压油微泄漏、密封垫损坏等小故障。液压驱动产生的噪音一般在75dB以上,宁夏科技馆利用设备在距离飞机3米左右的单独设备之间放置液压缸和油泵等,以阻断液压泵工作时的噪音。 四三自由度伺服电动气缸平台在展品中的应用 “血管漫游”展览从2017年开始启动,通过三自由度电动平台和VR设备实时模拟虚拟场景的变化,给人一种在血液中游泳的感觉。 展览由VR设备、控制主机、三自由度伺服电动缸平台座椅、耳机、一体头盔、游戏体验馆建设机构、液晶电视等7部分组成。 图4中的座位上挂着黑线,VR眼镜数据线长度有限。要求电脑主机要放在尽可能近的地方。选择三自由度伺服电动缸作为运动平台,其结构相对简单,因此有足够的空间部署计算机主机。同时,该展品是模拟血管内漫游的展品,有三个自由度,可以满足运动需求。 5结论 多自由度并行平台的应用可以很好地实现设计师的意图。特别是在模拟模拟展品中,能给观众带来良好的互动体验,这种展品在保证对游客持续吸引力的同时,便捷的可维护性、优秀的技术性能,在大型模拟科普展览项目中,多自由度平台的应用越来越广泛。 [b]创芯为电子[/b]为不同规模的企业提供[url=https://www.szcxwdz.com]电子元器件[/url]采购的平台。主要产品包括电源管理芯片、处理器及微控制器、接口芯片、放大器、存储器 、逻辑器件、数据转换芯片、电容、二极管、三极管 、电阻、电感、[url=https://www.szcxwdz.com]晶振[/url]等,并提供相关的技术咨询。在售商品超60万种,原?或代理货源直供,绝对保证原装正品,并满?客??站式采购要求,当天订单,当天发货,还可免费供样![b][b] [/b][/b]
A类不确定度中自由度怎么确定?
不确定度评估中的自由度,大家如何考虑?
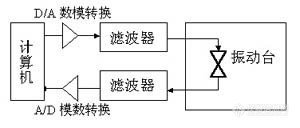
振动台闭环数控程序(以下简称:VibControl控制系统)是基于系统非线性迭代补偿理论来对控制信号和响应信号进行修正的。1.1 单自由度系统构成[img]http://ng1.17img.cn/bbsfiles/images/2009/11/200911230112_185926_1634361_3.jpg[/img]1.2 六自由度系统构成[img]http://ng1.17img.cn/bbsfiles/images/2009/11/200911230113_185927_1634361_3.jpg[/img]液压振动台其实就是电液伺服技术的进一步扩展,不过在高性能和大吨位的技术上远远高于电磁台的水平,如大型地震模拟系统和整个装甲车的振动模拟系统都是液压振动台.
日前,“十三五”国家重点研发计划“国家质量基础的共性技术研究与应用”重点专项“多自由度系统位置与姿态过程控制计量关键技术研究”项目实施方案论证会在中国计量科学研究院(简称“中国计量院”)召开。来自天津大学、中国科学院光电技术研究院、北京工业大学、北京理工大学、北京交通大学、北京航空航天大学等单位的院士和专家,中国计量院党委书记段宇宁、相关职能部门负责人以及项目参与单位技术骨干等参加论证会。[align=center][img]http://www.nim.ac.cn/sites/www.nim.ac.cn/files/news2018/07-09/image001_9.jpg[/img][/align][align=center]图1 论证会出席人员合影[/align] 项目负责人、中国计量院长度所薛梓研究员介绍了项目总体情况和实施方案,各课题负责人分别汇报了课题实施方案。 咨询专家组认真听取了汇报,重点针对项目自主研发的基标准装置、关键技术、关键设备的研发及应用等提出了质询。经讨论,与会专家一致认为项目实施方案目标明确、技术路线切实可行、保障措施有力,同意通过论证。[align=center][img]http://www.nim.ac.cn/sites/www.nim.ac.cn/files/news2018/07-09/image003_8.jpg[/img][/align][align=center]图2 论证会现场[/align] 中国计量院科技管理部、财务部管理人员及参与项目论证的财务专家分别就项目实施管理要求和经费使用要求进行了宣贯。 据介绍,随着中国制造业“机器换人”计划的实施,空间飞行器、航空母舰、核电机组等大型装备对制造质量的需求正在不断提升。多自由度非正交系统作为装备制造等领域控制质量和提高效率的关键,目前尚存在动态性能指标不准确、测量结果不一致等技术难题。为此,中国计量科学研究院牵头天津大学、浙江理工大学、北京航天计量测试技术研究所、中国航空工业集团北京长城计量测试技术研究所、杭州市质量监督检验检测研究院 、吉林省计量科学研究院、杭州新松机器人自动化有限公司等8家单位,联合开展有关研究,旨在攻克多自由度系统运动过程中的位置与姿态计量关键技术。 项目成果将有望服务于我国高端多自由度系统等制造和应用产业,解决高精度、多自由度设备的动态位置、姿态测量量值溯源问题,实现多自由度系统曲线轨迹的在线校准和补偿,提高测量速度,优化系统性能,带动国产多自由度系统向更大范围、更高精度的方向发展,助力我国多自由度系统的产品质量和国际竞争力提升。
MS(20)猫听说是方差大的自由度是横列,比如本例中就是MS(4)的自由度4,竖行是20,查表就是F(4,20)=2.87;-------------以上是不是正确的?----------好久没用.....猫有点老糊涂了,所以求助下网友
[size=3][font=Times New Roman]JJF1059[/font][font=宋体]中,第[/font][font=Times New Roman]5.12[/font][font=宋体]条指出:[/font][font=Times New Roman]B[/font][font=宋体]类不确定度分量的自由度与所得到的标准不确定度[/font][font=Times New Roman][i]u[/i]([i]x[sub]i[/sub][/i])[/font][font=宋体]的相对标准不确定度[/font][font=Times New Roman]σ{[i] u[/i]([i]x[sub]i[/sub][/i])}/[i] u[/i]([i]x[sub]i[/sub][/i])[/font][font=宋体]有关,其关系为:[/font][/size][size=3][i][font=Times New Roman]ν[sub]i[/sub][/font][/i][font=宋体]≈[/font][font=Times New Roman]1/2[[/font][font=宋体]Δ[/font][font=Times New Roman][i]u[/i]([i]x[sub]i[/sub][/i])/[i] u[/i]([i]x[sub]i[/sub][/i])][sup]-2[/sup][/font][/size][size=3][font=宋体]从文字叙述“标准不确定度[/font][font=Times New Roman][i]u[/i]([i]x[sub]i[/sub][/i])[/font][font=宋体]的相对标准不确定度”看起来,应该是标准不确定度[/font][font=Times New Roman][i]u[/i]([i]x[sub]i[/sub][/i])[/font][font=宋体]的不确定度,除以标准不确定度[/font][font=Times New Roman][i]u[/i]([i]x[sub]i[/sub][/i])[/font][font=宋体];但从表达式[/font][font=Times New Roman][[/font][font=宋体]Δ[/font][i][font=Times New Roman]u[/font][/i][font=Times New Roman]([i]x[sub]i[/sub][/i])/[i] u[/i]([i]x[sub]i[/sub][/i])][/font][font=宋体]中的[/font][font=宋体]Δ[/font][font=Times New Roman][i]u[/i]([i]x[sub]i[/sub][/i])[/font][font=宋体]看起来,却是标准不确定度[/font][font=Times New Roman][i]u[/i]([i]x[sub]i[/sub][/i])[/font][font=宋体]的增量,除以标准不确定度[/font][font=Times New Roman][i]u[/i]([i]x[sub]i[/sub][/i])[/font][font=宋体]。如果要表达标准不确定度[/font][font=Times New Roman][i]u[/i]([i]x[sub]i[/sub][/i])[/font][font=宋体]的相对标准不确定度,我觉得应该是:[/font][font=Times New Roman][i]u[/i]([i]u[/i]([i]x[sub]i[/sub][/i]))/[i] u[/i]([i]x[sub]i[/sub][/i])[/font][font=宋体]才对呀![/font][/size][size=3][font=宋体]请问实际上规范的本意是标准不确定度[/font][font=Times New Roman][i]u[/i]([i]x[sub]i[/sub][/i])[/font][font=宋体]的相对标准不确定度,还是标准不确定度[/font][font=Times New Roman][i]u[/i]([i]x[sub]i[/sub][/i])[/font][font=宋体]的增量,除以标准不确定度[/font][font=Times New Roman][i]u[/i]([i]x[sub]i[/sub][/i])[/font][font=宋体]。[/font][/size][size=3][font=宋体]还有该标准不确定度[/font][font=Times New Roman][i]u[/i]([i]x[sub]i[/sub][/i])[/font][font=宋体]的标准不确定度[/font][font=Times New Roman][i]u[/i]([i]u[/i]([i]x[sub]i[/sub][/i]))[/font][font=宋体]和标准不确定度[/font][font=Times New Roman][i]u[/i]([i]x[sub]i[/sub][/i])[/font][font=宋体]的增量[/font][font=宋体]Δ[/font][font=Times New Roman][i]u[/i]([i]x[sub]i[/sub][/i])[/font][font=宋体],应该说都不具可操作性(不好求得哦!),要说可能标准不确定度[/font][font=Times New Roman][i]u[/i]([i]x[sub]i[/sub][/i])[/font][font=宋体]的增量[/font][font=宋体]Δ[/font][font=Times New Roman][i]u[/i]([i]x[sub]i[/sub][/i])[/font][font=宋体]还稍好得一点点![/font][/size]
仔细看了下 HJ 168-2010 环境监测 分析方法标准制修订技术导则 里面方法检出限,若空白未检出目标物,要先估计个检出限,调整两次估计值用合并自由度公式计算。那么估计值刚好在检出限的2-5倍,还需要再估计个值用合并自由度来算呢?还是可以用前面那个公式 即MDL=t(n-1,0.99)×S 来算?
[b]‘有奖问答’对错题’:根据两个变量的18对观测数据建立一元线性回归方程。在对回归方程作检验时,残差平方和的自由度为( )。A[font=宋体]、[/font]18 B[font=宋体]、[/font]17C[font=宋体]、[/font]16 D[font=宋体]、[/font]1[/b]
[align=center][color=#17358f]什么叫标准物质的不确定度?[/color][/align][align=center][color=#17358f][color=#07519a]【来源/作者】岳小雨[/color][/color][/align][align=center][color=#17358f][color=#07519a][/color][/color][/align]关于“标准物质的不确定度”你了解多少呢?今天奥科就给大家普及一点这方面的小常识。首先,我们先从概念上了解不确定度:表征合理地赋予被测量之值的分散度,与测量结果相联系的参数。从定义可以看出,不确定度是对测量结果而言的,是用来表征结果的分散程度的,因此它可以用定量的数字来描述,即它是一个定量概念。对于标准物质来说,其不确定度结果由三部分组成:标准物质的不均匀性引起的不确定度、标准物质的不稳定性引起的不确定度和标准物质的定值过程带来的不确定度。将定值不确定度与均匀性、稳定性检验引入的不确定度按照平方和开方的方法叠加就给出合成标准不确定度,记为 uc。该合成标准不确定度乘以因子(该因子称为包含因子)得出的不确定度称为扩展不确定度或称总不确定度,记为 U。在给出扩展不确定度时应指明包含因子(记为 k)的数值,该值与要求的置信概率与自由度有关。[align=center][img=奥科标准物质不确定度]http://www.bzwz.com/UploadFile/20177614497237.png[/img][/align][color=#17358f][/color]
[img]http://www.instrument.com.cn/bbs/images/affix.gif[/img][url=http://www.instrument.com.cn/bbs/download.asp?ID=48996]柴油车自由加速烟度排放标准[/url]
校准证书中测量不确定度的表述应依据国家计量技术规范JJF 1059.1-2012《测量不确定度评定与表示》,使用的术语符号应与该技术规范相一致,遵循该技术规范对测量不确定度的报告与表示的规定。同时需注意以下几点: 1、在校准证书中给出的测量不确定度,必须指明是合成标准不确定度,还是扩展不确定度,以及对应于校准结果的具体参数。 例如:示值误差测量结果的扩展不确定度为..... =交流电压校准值xxV的扩展不确定度为.... 2、当被校准结果有多个同等重要的参数时,应分别给出各个参数的测量结果不确定度。 3、当测量结果的测量不确定度在整个测量范围内差异不大时,在满足量值传递要求的前提下,整个测量范围内的测量不确定度可取最大值。其最大值点的位置可能在测量范围的上限点也可能在测量范围的下限点或其他部位,要根据具体情况进行分析。 当整个测量范围的测量不确定度有明显的差异或有变化规律时,不能以一个值代表整个测量范围的不确定度,而应以函数形式或分段给出,或每个校准点都给出相应的测量不确定度。 4、当被校准的对象是计量标准器具,且测量结果的可能值接近正态分布时,应通过估算有效自由度, 取适当的包含概率,查表得t分布临界值Kp ,求得扩展不确度。在校准证书上应给出扩展不确定度,和包含概率 p,以及有效自由度的值,以便使用该计量标准器具进行下一级检定或校准时评定测量不确定度时引用。当不估算自由度直接取K值(通常取k=2)得到扩展不确定度时,应在校准证书上同时给出扩展不确定度和包含因子的值。 5、校准证书中的扩展不确定度只保留 1 位或 2 位有效数字。当第 1位有效数字是1或2时最好保留 2位有效数字。其余情况可以保留 1 位或2 位有效数字。保留的末位有效数字后面一位非零数字的舍入,比较保险的做法是只入不舍。 6、测量结果与其扩展不确定度的修约间隔应相同,即对测量结果数值进行修约时,其末位应与扩展不确定度的末位对齐。
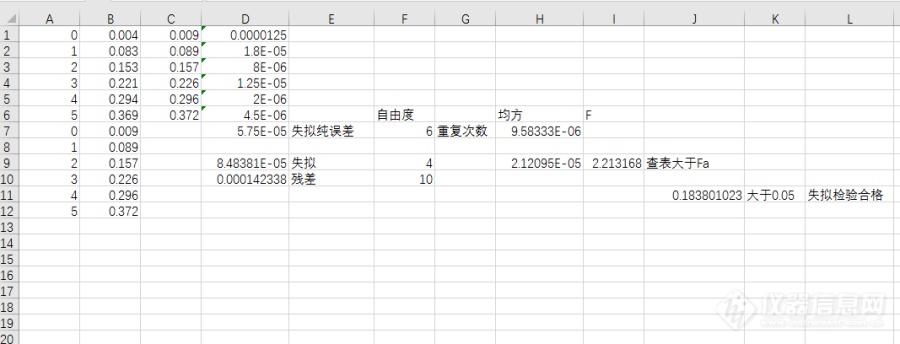
看了论坛专家calfstone 的帖子 标准曲线到底如何检验?[url]https://bbs.instrument.com.cn/topic/3467111[/url] 引起了很大的兴趣,他是利用Minitab的软件,进行标准曲线的检验。我想Minitab软件不熟,平常用的多的是EXCEL 设计模板能用它来检验标准曲线那就是方便很多了,而且非常实用。 我用的是EXCEL2016 版,分析数据参照calfstone 的帖子数据。标准曲线检验主要是线性检验(p0.05),以及残差的正态性检验,这样才是在统计学上比较完备的。线性检验与残差正态性检验利用EXCEL 回归功能,主要是推导出失拟检验的公式。[img=,690,207]https://ng1.17img.cn/bbsfiles/images/2019/10/201910101703394687_3336_2103464_3.png!w690x207.jpg[/img] 做失拟检验必须要有重复实验数据。在表sheet1输入A1-A12 为浓度 单位 mg/L ,B1-B12 为吸光度 C1-C6为重复实验的吸光度 等同于B7-B12 因为EXCEL不允许同时选两列作为y轴,所以这样排列。点击数据分析里选择回归,选择B1-B12 ,A1-A12 进行线性回归,同时选中残差,标准残差,残差图,线性拟合图,正态概率图。输出至sheet2[img=,403,227]https://ng1.17img.cn/bbsfiles/images/2019/10/201910101624487137_2756_2103464_3.png!w403x227.jpg[/img][img=,690,335]https://ng1.17img.cn/bbsfiles/images/2019/10/201910101628314897_430_2103464_3.png!w690x335.jpg[/img][img=,690,427]https://ng1.17img.cn/bbsfiles/images/2019/10/201910101633108936_1188_2103464_3.png!w690x427.jpg[/img] 这里斜率,截距,相关系数,方差,残差,概率等很多参数一目了然。 首先检验线性: x Variable(斜率) 的p(概率)为7.42E-17 远小于0.05 即回归是显著的。 截距(Intercept)检验的p 为0.000504 小于0.05 即截距不为0 其次是失拟检验:原理是要看曲线拟合后剩下残差与实验数据本身随机误差之间的差别,采用F检验,此时失拟检验P应该0.05,也就是说残差应该跟实验测定中的随机误差没有差别。sheet1中D1 输入=SUMSQ(B1:C1)-2*AVERAGE(B1:C1)^2 拉到D6 。在D7输入=SUM(D1:D6)即为纯误差平方和 其自由度为重复实验次数6。 D10,F10分别为 sheet2 中方差分析中残差平方和,自由度。D9,F9分别为失拟平方和(残差平方和减去纯误差平方和D10-D7),和自由度( 残差自由度减去纯误差自由度F10-F7)。 H7,H9为均方即 纯误差平方和 ,失拟平方和与各自自由度之比。这时可以用F检验 F为 H9/H7(失拟均方与纯误差均方之比)结果为2.213 查表在a=0.05 自由度4,6时F 临界值4.534。F小于临界值即在0.05的水平下,失拟的证据,并不显著。 F检验要查表有些麻烦,可以用p值检验法无需查表,利用EXCEL 的[color=#333333]FDIST函数(是返回两组数据的F概率分布的函数)[/color]FDIST(I9,F9,F7) 得到J11 的p为0.1838 大0.05 所以失拟检验合格。 最后残差的正态性检验:看sheet2 残差图和正态概率图,其中[color=#333333]正态概率图[/color][color=#333333]用于检查一组数据是否服从正态分布。是实数与正态分布数据之间函数关系的[/color][color=#333333]散点图。如果这组实数服从正态分布,正态概率图将是一条直线[/color][color=#333333]。图中散点基本上在一直线[/color]符合正态性。 参 考 文 献 (1) GB/T 22554-2010 基于标准样品的线性校准 附件是我做的EXCEL模板,欢迎指正。
头孢拉定胶囊含量测定结果不确定度评定 1测定方法:中国药典2000年版二部头孢拉定胶囊的含量测定,按中国药典2000年版附录ⅤD高效液相色谱法中的外标法测定。2数学模型 含量(%)=Cx×V100×W0×FA×100%Wx×P式中:CX= f×AX; f = WS/(V25×AS)Cx(mg/ml):供试品溶液浓度;V100(ml):100ml单标线容量瓶体积;V25(ml):25ml单标线容量瓶体积;W0 (g):胶囊的平均装量;Wx(g):供试品重量;WS(mg):对照品重量;P(mg):标示量;FA:含量的A类标准不确定度因子(FA=1.0);f:校正因子;AX:供试品峰面积;AS:对照品峰面积3因果图分析 重复性 WS 重复性 重复性 Cx f 校准 校准 AX 温度 校准 AS V25 含量(%) 重复性 重复性 W02 W01 温度 Wx1 Wx0 校准 校准 校准 校准 校准 重复性 V100 Wx W0 FA4方差(相对不确定度计算)u2rel(含量)= u2rel(Cx) + u2rel(V100) + u2rel(W0) + u2rel(FA) + u2rel(Wx) u2rel(Cx) = u2rel(fA) + u2rel(Ax) + u2rel(WS) + u2rel(AS)+ u2rel(V25)式中:urel(x)为变量x的相对标准不确定度5相对不确定度分量评定5.1100ml单标线容量瓶(A级):1. 体积:容量允差为±0.10ml (参照JJG 196-1990)体积的标准不确定度:u1=0.10/ =0.0577ml2. 温度:实验温度为(23±2)℃,溶液体积膨胀系数为2.1×10-4.℃-1假设温度分布为矩形分布,25ml体积的标准不确定度:u2=100×2.1×10-4×2/ =0.0242ml100ml单标线容量瓶(A级)的B类相对标准不确定度:urel(V100)=( u12+ u22)1/2/100=6.26×10-4γ1 = 50 (γ1:自由度,假设可信度为90%)5.225ml单标线容量瓶(A级):1. 体积:容量允差为±0.03ml (参照JJG 196-1990)体积的标准不确定度:u3=0.03/ =0.0173ml2. 温度:实验温度为(23±2)℃,溶液体积膨胀系数为2.1×10-4.℃-1假设温度分布为矩形分布,25ml体积的标准不确定度:u4=25×2.1×10-4×2/ =0.0069ml25ml单标线容量瓶(A级)的B类相对标准不确定度:urel(V25)= ( u32+ u42)1/2/25=7.45×10-4γ2 = 50 (γ2:自由度,假设可信度为90%)5.3Wx和W0的不确定度评定:A类相对标准不确定度(W0):S=2.67×10-3g;W0=03039guA(W0)= S/ =5.97×10-4 gurel(W0)1= uA (W0)/ W0=1.96×10-3γ3 =n-1=19 (γ3:自由度)式中:uA(x)为分量x的A类标准不确定度B类相对标准不确定度(天平):分度值:0. 1mg, B类不确定度u5=0.0577mg(矩形分布)载荷量最大误差:0.6mg, B类不确定度u6=0.2449mg(三角形分布)重复性误差:0.1mg, B类不确定度u7=0.0408mg(n=6,对W0 在A类标准不确定度中已评定此分量)urel(W0)2=( 2×(u52+ u62))1/2/ W0min=1.19×10-3 γ4 = 50 (γ4:自由度,假设可信度为90%)urel(Wx)= (2×( u52+ u62+ u72))1/2/ Wxmin=4.18×10-3 γ5 = 50 (γ5:自由度,假设可信度为90%)5.4Ws的不确定度评定(天平):分度值:0. 01mg, B类不确定度u8=0.0058mg(矩形分布)载荷量最大误差:0.04mg, B类不确定度u9=0.0163mg(三角形分布)重复性误差:0.03mg, B类不确定度u10=0.0122mg(n=6)urel(Ws)= (2×(u82+ u92+ u102))1/2/ Wsmin =1.64×10-3 γ6 = 50 (γ6:自由度,假设可信度为90%)5.5fA的不确定度评定(SP法)校正因子的测定结果:序列123平均值S对照液18.08588×10-58.06822×10-58.08628×10-58.0801×10-51.029×10-7对照液28.05532×10-58.05694×10-58.05842×10-58.0567×10-51.55×10-8SP=((S12+S22)/2)1/2=0.736×10-7urel(fA)=0.736×10-7×2/(8.0801×10-5+8.0567×10-5)/ = 5.27×10-4γ7 = 2×(3-1)= 4 (γ7:自由度)5.6AS 和Ax的不确定度评定(只考虑重复性)urel(AS) =0.28%/ =1.14×10-3 γ8 =n-1=5 (γ8:自由度)urel(Ax) =0.28%/ =1.14×10-3 γ9 =n-1=5 (γ9:自由度)5.7FA的不确定度评定(测定结果的A类相对标准不确定度)含量测定结果平均值:102.2% S=0.46%urel(FA)=0.46%/(61/2×102.2%)=1.84×10-3 γ10 =n-1=5 (γ10:自由度)6相对标准不确定度一览表序号相对标准不确定度自由度来源符号数值符号数值1定容urel(V100)6.26×10-4γ1502urel(V25)7.45×10-4γ2503称量urel(W0)11.96×10-3γ3194urel(W0)21.19×10-3γ4505urel(Wx)4.18×10-3γ5506urel(Ws)1.64×10-3γ6507校正因子urel(fA)5.27×10-4γ748积分urel(AS)1.14×10-3γ859urel(Ax)1.14×10-3γ9510重复性urel(FA)1.84×10-3γ1057相对合成标准不确定度urel(含量)=(6.262+7.452+19.62+11.92+41.82+16.42+5.272+11.42+11.42+18.42)1/2×10-4=5.72×10-38有效自由度(γeff)γeff=57.246.264+7.454+19.64+11.94+41.84+16.44+5.274+11.44+11.44+18.445050195050504555 =1069扩展不确定度取p=95%,γeff=106,在t分布下k=1.984Uk=1.984×5.72×10-3×102.2%=1.2%10测量不确定度报告测定结果:含量(%)=102.2%±1.2% (±符号后为扩展不确定度,k=1.984,p=95%)
维生素E胶丸含量测定结果不确定度评定 1测定方法:中国药典2000年版二部维生素E胶丸的含量测定,按中国药典2000年版附录ⅤE[url=https://insevent.instrument.com.cn/t/Mp]气相色谱[/url]法中的内标法测定。2数学模型 含量(%)=Cx×V10×W0×FA×100%Wx×P式中:CX=(f×AX×CR)/AR ; f = (AR×Cs) /(CR×AS); Cs= WS / V10Cx(mg/ml):供试品溶液浓度;V10(ml):10ml单刻度吸管体积; W0 (g):胶囊的平均装量;Wx(g):供试品重量;WS(mg):对照品重量;P(mg):标示量;FA:含量的A类标准不确定度因子(FA=1.0);f:校正因子;AX:供试品峰面积;AS:对照品峰面积;CR(mg/ml):内标溶液浓度;CS(mg/ml):对照品溶液浓度;AR:内标物峰面积3因果图分析 WS 重复性 Cx 校准 重复性 AX f 温度 校准 AR AR AS V10 含量(%) W02 W01 温度 重复性 校准 校准 校准 校准 重复性 V10 Wx W0 FA4方差(相对不确定度计算)u2rel(含量)= u2rel(Cx) + u2rel(V10) + u2rel(W0) + u2rel(FA) + u2rel(Wx) u2rel(Cx) = u2rel(fA) + u2rel(Ax) + u2rel(AR) + u2rel(AS) + u2rel(AR) + u2rel(WS) + u2rel(V10)u2rel(含量)= u2rel(fA) + u2rel(Ax) + u2rel(AR) + u2rel(AS) + u2rel(AR) + u2rel(WS) + u2rel(V10) + u2rel(V10) + u2rel(W0) + u2rel(FA) + u2rel(Wx)式中:urel(x)为变量x的相对标准不确定度5相对不确定度分量评定5.110ml单标线吸管(A级):1. 体积:容量允差为±0.020ml (参照JJG 196-1990)体积的标准不确定度:u1=0.020/ =0.0115ml2. 温度:实验温度为(23±2)℃,溶液体积膨胀系数为2.1×10-4.℃-1假设温度分布为矩形分布,25ml体积的标准不确定度:u2=10×2.1×10-4×2/ =0.00242ml10ml单标线容量瓶(A级)的B类相对标准不确定度:urel(V10)=( u12+ u22)1/2/10=1.18×10-3γ1 = 50 (γ1:自由度,假设可信度为90%)5.2Wx、W0和Ws的不确定度评定:A类相对标准不确定度(W0):S=3.17×10-3g;W0=0.2451guA(W0)= S/ =7.09×10-4 gurel(W0)1= uA (W0)/ W0=2.89×10-3γ2 =n-1=19 (γ2:自由度)式中:uA(x)为分量x的A类标准不确定度B类相对标准不确定度(天平):分度值:0. 1mg, B类不确定度u3=0.0577mg(矩形分布)载荷量最大误差:0.4mg, B类不确定度u4=0.1633mg(三角形分布)重复性误差:0.1mg, B类不确定度u5=0.0408mg(n=6,对W0 在A类标准不确定度中已评定此分量)urel(W0)2=( 2×(u32+ u42))1/2/ 20/W0=5.0×10-5 γ3 = 50 (γ3:自由度,假设可信度为90%)urel(Wx)= ( u32+ u42+ u52)1/2/ Wxmin=3.39×10-3 γ4= 50 (γ4:自由度,假设可信度为90%) urel(Ws)= ( u32+ u42+ u52)1/2/ Wsmin=6.90×10-3 γ5= 50 (γ5:自由度,假设可信度为90%)5.3AS、 AR和Ax的不确定度评定(只考虑重复性)、urel(AS) =0.72%/ =2.94×10-3 γ6 =n-1=5 (γ6:自由度)urel(AR) =0.72%/ =2.94×10-3 γ7 =n-1=5 (γ7:自由度)urel(Ax) =0.72%/ =2.94×10-3 γ8 =n-1=5 (γ8:自由度)5.4fA的不确定度评定(SP法)校正因子的测定结果:序列123平均值S对照液11.216441.215301.215021.21567.522×10-4对照液21.219471.219451.218451.21915.832×10-4SP=((S12+S22)/2)1/2=9.518×10-4urel(fA)= 9.518×10-4×2/(1.2156+1.2191)/ = 4.51×10-4γ9 = 2×(3-1)= 4 (γ9:自由度)5.5FA的不确定度评定(测定结果的A类相对标准不确定度)含量测定结果平均值:98.5%; S=0.33%urel(FA)=0.33%/61/2/98.5%=1.37×10-3 γ10 =n-1=5 (γ10:自由度)6相对标准不确定度一览表序号相对标准不确定度自由度来源符号数值符号数值1定容urel(V10)1.18×10-3γ1502urel(V10)1.18×10-3γ1503称量urel(W0)12.89×10-3γ2194urel(W0)25.0×10-5γ3505urel(Wx)3.39×10-3γ4506urel(Ws)6.90×10-3γ5507积分urel(AS)2.94×10-3γ658urel(AR) 2.94×10-3γ759urel(AR) 2.94×10-3γ7510urel(Ax)2.94×10-3γ8511校正因子urel(fA)4.51×10-4γ9412重复性urel(FA)1.37×10-3γ1057相对合成标准不确定度urel(含量)=(11.82+11.82+28.92+0.52+33.92+69.02+29.42+29.42+29.42+29.42+4.512+13.72)1/2×10-4=1.04×10-28有效自由度(γeff)γeff=104411.84+11.84+28.94+0.54+33.94+69.04+4×29.44+4.514+13.74505019505050545 =1049扩展不确定度取p=95%,γeff=104,在t分布下k=1.984Uk=1.984×1.04×10-2×98.5%=2.1%10测量不确定度报告测定结果:含量(%)=98.5%±2.1% (±符号后为扩展不确定度,k=1.984,p=95%)
JJF1133-2005 X射线荧光光谱法黄金含量分析仪校准规范的附录A有几个疑惑:1、表A-2的标样的不确定度50如何得来?2、有效自由度的取法是只进不舍吗?比如按照校准给的规范算得的有效自由度为49.43,结果取了503、给定置信水平p=0.99,有效自由度为50,查t分布得覆盖因子k=t0.99(50)=2.68,为什么我查的结果是2.40?
阿昔洛韦片含量测定的不确定度评定1.测量方法:中华人民共和国卫生部部标准WS3-(X-033)-932中的含量测定,阿昔洛韦的吸 收系数(E1%1cm=622)2.数学模型:Cx(含量%)=Ax×V250×V100×1%× W0 ×FA×100%V5×E1%1cm×Wx×PAx:样品吸收值; W0:平均片重;V250:250ml容量瓶体积; V100:100ml容量瓶体积;V5:单标线吸管体积; Wx:样品称重量;P:标示量; FA:A类标准不确定度因子(FA=1)3.因果图分析: E1%1cm W0 AX FA 重复性 校准 含量(%) 重复性 重复性 V5 Wx1 Wx0 V100 校准 温度 V250 校准 校准 重复性校准 温度 校准 温度 Wx 稀释4.方差(相对不确定度计算公式):U2Rel(Cx)=U2Rel(Ax)+U2Rel(V250)+U2Rel(V100)+U2Rel(V5)+U2Rel(E1%1cm)+U2Rel(W0)+ U2Rel(Wx) +U2Rel(FA)式中:urel(x)为变量x的相对标准不确定度5.标准不确定度评定(分量):5.1 250ml单标线容量瓶(A级):1.体积:容量允差为±0.15ml(参照JJG-196-1990)体积的标准不确定度:u1=0.15/31/2=0.0866ml2.温度:实验温度为(23±2)oC,溶液体积膨胀系数为2.1×10-4/ oC 假设温度分布为矩形分布,250ml单标线容量瓶不确定度 u2=250×2.1×10-4×2/31/2=0.0606ml 250ml单标线容量瓶的B类相对标准不确定度 URel(V250)=(u12+u22)1/2/ V250=4.23×10-4 γ1 = 50 (γ1:自由度,假设可信度为90%)5.2 100ml单标线容量瓶(A级):1.体积:容量允差为±0.10ml(参照JJG-196-1990)体积的标准不确定度:u3=0.10/31/2=0.0577ml2.温度:实验温度为(23±2)oC,溶液体积膨胀系数为2.1×10-4/ oC 假设温度分布为矩形分布,250ml单标线容量瓶不确定度 u4=100×2.1×10-4×2/31/2=0.02425ml 100ml单标线容量瓶的B类相对标准不确定度 URel(V100)=(u32+u42)1/2/ V100=6.26×10-4 γ2 = 50 (γ2:自由度,假设可信度为90%) 5.3 5ml单标线吸管(A级):1.体积:容量允差为±0.015ml(参照JJG-196-1990)体积的标准不确定度:u5=0.015/31/2=0.00866ml2.温度:实验温度为(23±2)oC,溶液体积膨胀系数为2.1×10-4/ oC 假设温度分布为矩形分布,250ml单标线容量瓶不确定度 u6=5×2.1×10-4×2/31/2=0.00121ml 5ml单标线吸管的B类相对标准不确定度 URel(V5)=(u52+u62)1/2/ V5=2.98×10-3 γ3 = 50 (γ3:自由度,假设可信度为90%) 5.4 Wx和W0的不确定度评定:W0的A类标准不确定度(n=20):S=0.00492g, W0=0.3284g UA(W0)=S/201/2=1.10mgUrel(W0)1= uA (W0)/ W0=3.35×10-3γ4 =n-1=19 (γ4:自由度)式中:uA(x)为分量x的A类标准不确定度B类相对标准不确定度(天平): 最大误差:0.4mg,B类不确定度u7=0.1633mg(三角分布) 实际分值:0.1mg,B类不确定度u8=0.0577mg(矩形分布)重复性误差:0.1mg,B类不确定度u9=0.0408mg(n=6,对W0 在A类标准不确定度中已评定此分量)Urel(W0)2=(u72+ u82)1/2/ W0min=5.42×10-3 γ5 = 50 (γ5:自由度,假设可信度为90%)Urel(Wx)= (2×( u72+ u82+ u92))1/2/ Wxmin=3.87×10-3 γ6 = 50 (γ6:自由度,假设可信度为90%)5.5E1%1cm的不确定度评定:E1%1cm的允差:1Urel(E1%1cm)= 1/31/2/ 622=9.28×10-4 γ7= 200 (γ7:自由度,假设可信度为95%)5.6Ax的不确定度评定:透射比的不确定度:0.5%(T)A=-logT(-logT)’=1/(Tln10)=0.4343×10Au(A)= 0.4343×10A×u(T)/31/2=0.00389Urel(Ax)=7.91×10-3γ8 = n-1=5 (γ8:自由度)5.7FA的不确定度评定(测定结果的A类相对标准不确定度)含量测定结果平均值:99.6%, S=0.52%urel(FA)=0.52%/(61/2×99.6%)=2.13×10-3 γ9=n-1=5 (γ9:自由度)6.相对标准不确定度一览表序号相对标准不确定度自由度来源符号数值符号数值1定容URel(V250)4.23×10-4 γ1502URel(V100)6.26×10-4γ2503URel(V5)2.98×10-3γ3504称量Urel(W0)13.35×10-3γ4195Urel(W0)25.42×10-3γ5506Urel(Wx)3.87×10-3γ6507吸收系数Urel(E1%1cm)9.28×10-4γ72008吸收度Urel(Ax)7.91×10-3γ859重复性urel(FA)2.13×10-3γ957.相对合成标准不确定度URel(Cx) =(4.232+6.462+29.82+33.52+54.22+38.72+9.282+79.12+21.32)1/2×10-4= 1.16×10-28.有效自由度(γeff)γeff=11644.234+6.464+29.84+33.54+54.24+38.74+9.284+79.14+21.3450505019505020055 =22.29.扩展不确定度取p=95%,γeff=22.2,在t分布下k=2.077Uk=2.077×1.16×10-2×99.6%=2.4%10.测量不确定度报告测定结果:含量(%)=99.6%±2.4% (±符号后为扩展不确定度,k=2.077,p=95%)

GUM法评定不确定度时认为:分析结果符合正态分布,依据各个分量通过测试模型来计算得到分析结果;利用方差传播定理和测试模型来计算分析结果的标准差s;通过各分量不确定度和自由度计算分析结果分布的自由度n,然后在给定的置信概率下,确定包含因子K,最后按照要求把评定结果表示出。 http://ng1.17img.cn/bbsfiles/images/2016/08/201608221012_606083_1898299_3.png可以参考这个ppt,不明白的去学学数理统计,包含因子,扩展不确定度等就都弄清楚了。
测量不确定度的评估程序 1 目的及适用范围1.1 为正确评价测量的不确定度,保证测量结果的有效性,制定本程序。1.2 本程序适用于实验室测量不确定度的评估活动。2 职责本程序由质量负责人组织实施。3 工作程序3.1 测量不确定度是对测量结果的不可信程度或对测量结果有效性的怀疑程度。测量不确定度的评定与表达方式,按国家计量技术规范JJF1059-1999《测量不确定度评定与表示》的要求进行。3.2 测量不确定度的来源。测量不确定度一般来源于以下因素:a. 被测量的定义不完整;b. 复现被测量的测量方法不理想;c. 取样的代表性不能代表所定义的被测量;d. 对测量过程受环境影响的认识不恰如其分或对环境的测量与控制不完善;e. 对模拟式仪器的读数存在人为偏移;f. 测量仪器的计量性能(如灵敏度、鉴别力、分辨力及稳定性等)的局限性;g. 测量标准或标准物质的不确定度;h. 引用的常数或参数的不确定度;i. 测量方法、测量系统和测量程序引起的不确定度;j. 被测量的各种随机影响,使测量时重复观测值的变化。3.3 评估方法3.3.1 A类标准不确定度的评估方法对于被测量y,在同一条件下进行的n次平行测定,由下式计算测定结果的标准偏差:S(y)= (yi-y)2/(n-1) 如果以y作为被测量值Y的估计值(即测定结果),均数的标准差S(y)即为测定结果的标准不确定度u(y): s(y) (yi-y)2u(y)=S(y)= = n n(n-1) 如果在复现条件下,将前述平行测定进行了m次复现实验(如质量控制图),则可用合并标准偏差SP表征:若每次核查的自由度相等,即等权时: Sj2Sp= 其中:Sj2= (xi-x)2/(n-1) P不等权时: vjsj2 Sp= 其中: Vj 为自由度 vj在这种情况下,如果以n次测定结果的平均值Y作为测定结果时,其标准不确定度为:u(x)=Sp/ 3.3.2 B类标准不确定度的评估B类评定时的信息来源:a 以前测量的数据;b 经验和对有关仪器性能或材料特性的一般知识;c 生产厂的技术说明书;d 检定/校准证书、测试报告或其它提供数据的文件;e 引用的手册。一般根据经验或有关信息和资料,分析判断被测量的可能值区间(-a,a),并假设被测量值的概率分布,由要求的置信水平,估计包含因子k,则测量不确定度ux为: ux=a/k k ……包含因子。3.3.3 合成标准不确定度的评定合成标准不确定度uc(y)通常采用方和根法(必要时要考虑协方差),当被合成分量彼此独立(不相关)时: uc2(y)= u2i(y)当测量结果y由测得量X按评定模型y=f(x) 算出时,xi的标准不确定度,须乘以传播系数 , 即: ui= u(xi)3.3.4 扩展不确定度的评定扩展不确定度u由合成不确定度乘以包含因子k得到: u=kuc(y)3.3.5 结果表示测量结果可表示成y=y±u(即y-u≤y≤y±u),K值大多数取2~3,一般情况下取2。k值也可以根据被测量y的概率分布,在确定相应的置信水平(通常采用P=%95)下,从一定的自由下,从相应的统计表上查得。自由度veff 由下式得出: uc4(y)Veff = 其中:Ci= f/ x Ci4u4(xi) vi如果所有的u(xi)是独立的分量,则:Veff = vi3.4 如果采用的被广泛公认的测试方法规定了测量不确定度主要来源的极限值并规定了计算结果的表示形式,在这种情况下,实验室遵守该测试方法和报告要求即被认为符合本程序要求。3.5 除非客户要求、规定需要或特殊的检测项目,本实验室一般不出具不确定度报告。相关文件HTQ-4-A-051 测量不确定度的评定实例(抄别人的东西,公式都没抄好!对不起大家了!)
一、测量不确定度基础知识 1. 什么是测量不确定度? 2. 为什么要采用测量不确定度? 3. 测量不确定度与测量误差有何联系与区别? 4. 测量不确定度的来源有哪些? 5. 如何理解"被测量的定义不完整"? 6. 我国关于测量不确定度有哪些规定? 7. 采用测量不确定度对检测和校准工作有什么好处? 8. 国际上采用测量不确定度的情况如何? 9. 进行计量认证或实验室认可时必须要做不确定度评定吗? 10. 实验室有许多检测项目和参数,每一个参数又有不同的测量范围,那么应如何开展测量不确定度评定呢? 11. 在某些行业中,被测量的样品值的分散性较大,在进行测量不确定度评定时如何考虑样品分散性的影响? 12. 实验室现在做了测量不确定度评定,以后可以利用这些评定结果吗?如何利用? 13. 校准工作的测量不确定度评定与检测工作的测量不确定度评定有区别吗? 14. 检测实验室有时需要判定产品的符合性,这时需要考虑测量不确定度吗?二、随机变量的分布问题 15. 什么是随机变量?什么是离散型随机变量?什么是连续型随机变量? 16. "离散"和"分散"有何不同之处? 17. 什么是概率?什么是概率密度? 18. 置信度、置信水平、置信概率有何区别? 19. 什么是随机变量的分布?判别随机变量的分布有什么用? 20. 测量工作中有哪些常见的分布?这些分布各有哪些特征? 21. 如何判别随机变量属于何种分布? 22. 正态分布与t分布有何区别?什么情况下用正态分布,什么情况下用t分布? 24. t分布和学生分布是一回事吗? 23. 检定证书没有给出误差属于何种分布,也没给出其他信息,应如何处理? 24. 什么情况下是投影分布?如何计算投影分布的标准偏差? 25. 对同一被测量多次重复测量,单次测量示值的分布是正态分布吗?三、包含因子问题 26. 什么是包含因子?如何选取包含因子的值? 27. 在计算扩展不确定度的过程中,一定是用t分布表来计算包含因子吗?四、自由度问题 28. 什么是自由度? 29. 为什么要计算自由度?任何情况下都必须计算自由度吗? 30. 在B类评定时如何计算自由度?已知随机变量的分布时(正态分布和t分布除外),自由度就一定是∞吗? 31. 有多个被测量时如何计算自由度? 32. 什么是有效自由度? 如何计算有效自由度? 33. 什么是安全因子?如何计算安全因子?五、标准偏差问题 34. 什么是标准偏差?标准偏差有什么用? 35. 单次测量的标准偏差、平均值的标准偏差、合并样本的标准偏差有什么区别?各在什么情况下应用? 36. 如何求平均值的合并样本的标准偏差? 37. 单次测量的标准偏差与平均值的标准偏差的自由度是一样 的吗? 38. 不是正态分布的情况下如何计算标准偏差? 39. 什么是极差法?如何用极差法计算标准偏差?六、测量不确定度的评定方法问题 40. 测量不确定度的评定方法可分几类?A类不确定度评定和B 类不确定度评定有什么联系和区别? 41. A类不确定度评定都是随机效应的影响吗? B类不确定度评定都是系统效应的影响吗 42. 测量仪器有不确定度吗?测量方法有不确定度吗? 43. 什么情况下用A类评定?什么情况下用B类评定? 44. 任何情况下都必须有A类不确定度评定吗? 45. 如何进行A类不确定度评定? 46. 如何进行B类不确定度评定? 47. 从评定A类不确定度评定的角度来考虑,应如何安排重复性 或复现性试验? 48. 进行B类不确定度评时,就一定不涉及重复性或复现性试验 数据吗? 49. 在评定测量不确定度时,如何考虑仪器示值误差的影响? 50. 在评定测量不确定度时,如何考虑仪器系统误差的影响? 51. 在评定测量不确定度时,如何考虑重复性限、复现性限的影 响 52. 在评定测量不确定度时,如何考虑读数误差的影响? 53. 在评定测量不确定度时,如何考虑量化误差的影响? 54. 如何评估生产厂商所给的说明书中的技术指标? 55. 仪器的检定证书中只给出 "符合要求"这句话,怎么办? 56. 一台仪器有好几段量程,如何考虑不确定度的评定? 57. 有些仪器给出的误差后面有F.S的符号,是什么意思? 58. 经过检定/校准的仪器和未经过检定/校准的仪器,在考虑测量不确定度时有所不同吗? 59. "偏差"和"误差"有何区别? 60. 什么是分度值?可以用分度值代替误差吗? 61. 重复性和复现性有何区别?所谓 "相同的时间" 可以相同到什么程度? 62. 如何评定温度变化对不确定度的影响? 63. 在评定测量不确定度时,仪器误差的影响是否会被重复评定?如何避免重复评定? 64. 什么是参考标准?什么是标准物质?什么是有证标准物质? 65. 在已经知道约定真值的情况下,如何评定测量不确定度? 66. 对数学期望为零的两个量的乘积如何评定其合成不确定度?七、数学模型问题 67. 输入量、观测值、估计值、测量结果有什么区别? 68. 什么是数学模型?为什么要建立数学模型? 69. 如何建立数学模型? 70. 被测量的数学模型与不确定度的数学模型有何联系? 71. 对同一种方法来说,可以建立不同的不确定度的数学模型吗? 72. 对用最小二乘法回归的经验模型,如何评定不确定度? 73. 建立 "黑箱"型数学模型要注意什么问题?八、合成标准不确定度问题 74. 如何计算合成标准不确定度? 75. 什么是不确定度传播律 76. 什么是灵敏系数?如何计算灵敏系数? 77. 在JJG1059 -1999《测量不确定度评定与表示》中,脚标I、j、k各代表什么意思? 78. 输入量的标准不确定度、标准不确定度的分量、合成标准不 确定度、扩展不确定度、相对标准不确定度各有什么区别? 79. 在非线性数学模型的情况下,如何利用相对标准不确定度来简化计算? 80. 不确定度的分量中还可以有分量吗? 81. 什么是相关?如何计算相关系数? 82. 在有相关量的情况下,如何简化计算? 83. 用同一台仪器来测量两个输入量,如何考虑相关性问题? 84. 如何正确报告测量不确定度? 85. 在化学分析中,如何评定滴定的不确定度? 86. 在《化学分析中不确定度的评估指南》的表A2.1中 "rep"是什么意思?它的数值为何等于1.0?,它的标准不确定度是如何得到的? 87. 画因果图有何好处?如何画因果图? 88. 画不确定度分量的统计直方图有何好处? 89. 列表表示不确定度分量有何好处?九、检测方法问题 90. 什么是经验方法?什么是合理方法? 91. 什么是《方法确认》?为什么要进行方法确认? 92. 测量方法也有性能指标吗?用哪些参数评定测量方法的性能? 93. 什么是检测限? 94. 什么是方法的稳健性、选择性、交互灵敏度? 95. 如何进行方法确认? 96. 确认了的方法可以扩展吗?应如何扩展? 十、最佳测量能力问题 97. 什么是"最佳测量能力"? 98. 为什么要评定实验室的最佳测量能力?如何评定实验室的最佳测量能力?十一、符合性判定问题 99. 在进行产品对技术规范的符合性判定时,如何考虑测量不确定度的影响? 100. 为什么说质量检验机构进行符合性判定时是要承担风险的?如何计算风险有多大呢?
请各位同仁到资料中心下载 http://www.instrument.com.cn/download/shtml/062569.shtml测量误差与不确定度评定一、测量误差1、测量误差和相对误差(1)、测量误差(2)、相对误差2、随机误差和系统误差(1)、随机误差(2)、系统误差3、修正值和偏差(1)、修正值和修正因子(2)、偏差二、测量不确定度的评定与表示1、测量不确定度(1)测量不确定度来源(2)标准不确定度和标准[偏]差2.不确定度的A类、B类评定及合成 (1) 不确定度的A类评定 (2) 不确定度的B类评定 (3) 合成标准不确定度3.扩展不确定度和包含因子 (1)扩展不确定度 (2)包含因子和自由度4.测量不确定度的评定和报告 (1)测量不确定度的评定流程三、测量误差与测量不确定度范例:常用玻璃量器比对测量结果不确定度评定
1、定义误差:表明测量结果偏离参考量值,是一个确定的值。不确定度:表明被测量之值的分散性,是一个区间。 2、分类误差:按出现于测量结果中的规律分为随机误差和系统误差。不确定度:按是否用统计学方法求得,分为A类评定和B类评定,在评定时一般不区分其性质。若需要区分,应表述为“由随机(或系统)效应引入的不确定度分量”。 3、可操作性误差:由于参考量值未知,往往无法得到测量误差的值。不确定度:通过对实验、资料、经验等信息进行评定,可定量确定。 4、数值符号误差:非正即负。不确定度:不用正负号表示无符号,恒为正值。 5、合成方法 误差:各误差分量的代数和。不确定度:当各分量不相关时,用方和根法合成,否则应考虑加入相关项。 6、结果修正误差:已知系统误差的估计值时,可对测量结果进行修正。修正值等于负的系统误差。不确定度:为一个区间,因此无法用不确定度对结果进行修正;对已修正结果进行不确定度评定时,应考虑修正不完善引入的不确定度分量。 7、结果说明误差:误差客观存在,属于给定的测量结果,相同的测量结果具有相同的误差。不确定度:在相同条件下进行测量时,合理赋予被测量的任何值均具有相同的测量不确定度,即测量不确定度仅与测量过程有关。 8、实验标准偏差误差:来源于给定的测量结果。它不表示被测量估计值的随机误差。不确定度:来源于合理赋予的被测量之值,表示同一观测列中,任一个估计值的标准不确定度。 9、自由度 误差:不存在。不确定度:可作为不确定度评定可靠程度的指标。 10、包含概率 误差:不存在。不确定度:当了解分布时,可按包含概率给出包含区间。
测量误差与不确定度评定 一、测量误差 1、测量误差和相对误差 (1)、测量误差 (2)、相对误差 2、随机误差和系统误差 (1)、随机误差 (2)、系统误差 3、修正值和偏差 (1)、修正值和修正因子 (2)、偏差 二、测量不确定度的评定与表示 1、测量不确定度 (1)测量不确定度来源 (2)标准不确定度和标准[偏]差 2.不确定度的A类、B类评定及合成 (1) 不确定度的A类评定 (2) 不确定度的B类评定 (3) 合成标准不确定度 3.扩展不确定度和包含因子 (1)扩展不确定度 (2)包含因子和自由度 4.测量不确定度的评定和报告 (1)测量不确定度的评定流程 三、测量误差与测量不确定度 范例:常用玻璃量器比对测量结果不确定度评定 下载地址:http://www.instrument.com.cn/show/download/DownLoad_Free.asp?id=62569
请问物质的标准自由生成焓这些物性数据能在哪里查到?书名或是文献名一般叫什么先谢谢啦